13장. 통계적 품질관리

통계적 품질관리(Statistical Quality Control; SQC) - 1924년 슈하르트(W. shewahart)에 의해 소개된 이후 현재까지도 가장 보편적으로 사용되며 많은 산업체로부터 그 성능을 입증받음

SQC 또한 만능의 기법은 아니며 특히 공정에 중점을 둔 것으로 품질을 향상시키고자 하는 노력에는 한계가 있음

이에 최근에는 제품의 설계 분야에 보다 중점을 둔 다구찌 방법등이 등장하였지만 SQC는 여전히 기본적으로 필요한 수단

즉, 효율적인 공정관리의 바탕 위에서 다구찌 방법 등이 효과를 거둘수 있음

TQC(Total Quality Control) 또는 TQM(Total Quality Management) 의 경우 품질향상에 대한 노력을 조직 전체의 목표로 확장한 것이지만 중요한 부분 중 하나는 생산과 직결되는 공정상의 문제점 해결에 있음 $\Rarr$ SQC가 이에 중추적인 역할을 하고 있음

13.1 품질변동과 관리도

어느 생산공정에 있어서나 생산되는 제품의 품질은 제품별로 차이가 있음

충분히 설계되고 관리되는 공정이라 할지라도 완전히 동일한 품질의 제품을 생산하는 것은 현실적으로 불가능

$\rarr$ 생산공정에는 관리가 불가능한 많은 요인들이 존재하고 이들 요인들에 의한 품질의 변동은 불가피 하기 때문

이와 같은 불가피한 원인들을 우연요인(chance cause)라 하고 우연요인에 의한 품질변동이 크게 문제되지 않는다면 그러한 정도의 품질변동은 자연스러운 것으로 받아들일 수 있음

이와 반대로 공정이 관리상태를 이탈함으로써 품질변동이 발생하는 경우가 있음

이러한 요인들에 의한 변동의 폭은 우연요인에 의한 경우보다 상대적으로 큰 것이 보통

이와 같은 우연요인 이외의 변동요인을 이상요인(assignable cause)이라 함

공정에 이상요인이 발생한 경우 그 공정이 관리 상태를 이탈했다 또는 벗어났다고 말함

목표치에서 어느 정도 벗어난 것이 이상상태인지를 판단하기는 어려울 수 있음

여기에 통계적 기법이 큰 역할을 하게 됨

품질특성이 직경, 길이, 중량 등과 같이 측정가능한 것일 경우 이를 계속적으로 측정, 집계하면 공정의 목표치 부근에 떨어지는 경우가 많음

목표치에서 멀리 벗어나는 값을 갖는 경우 점점 작아지는 경향이 있음

따라서 많은 경우 공정의 품질특성이 정규분포를 따른다고 가정

정규분포곡선은 3.6.5절에서 다루었듯 평균과 표준편차의 두 모수에 의해 결정

표준편차는 보통 $\sigma$로 표시하며 분포의 퍼진 정도를 나타냄

공정이 정규분포를 따른다고 가정할 때 어떠한 품질특성치가 평균에서 $\pm \sigma$에 놓일 확률은 68.3%

평균에서 $\pm2\sigma$ 사이에 놓일 확률은 95.45%, $\pm3\sigma$에 놓일 확률은 99.73%

따라서 공정이 정규분포를 따른다고 가정할 때 $\pm3\sigma$밖으로 벗어나는 경우는 약 0.27%로 상당히 드문 경우에 속함

관리도에서 3-시그마 규칙을 사용하는 이유가 바로 여기에 있음

13.1.1 관리도의 원리

품질관리의 중요한 목적 중 하나는 공정에 이상요인이 발생하였을 경우 가능한 빨리 이를 탐지하여 수정조치를 취함으로써 불량제품의 발생을 사전에 억제하는 것

이러한 목적으로 가낭 널리 사용되는 대표적인 기법이 바로 관리도(control chart)

관리도는 품질의 변동상황을 그래프로 나타낸 것 공정에 대한 정보들(평균, 산포, 불량률 등)을 추정하거나 공정능력을 결정하는데 이용될 수 있고, 공정 개선을 위한 유익한 정보를 제공하기도 함

💡

관리도는 불량을 감지하고자 하는 것이 아니고 불량 발생 이전에 공정의 이상 상태를 감지하고자 고안된 것

관리도는 품질특성의 변화를 그래프로 나타낸 것

관리상태에서의 품질 특성치의 평균을 나타내는 중심선(center line; CL)과 관리상한선(upper control line; UCL) 및 관리하한선(lower control line; LCL)로 구성

💡

관리도 상의 문제는 이러한 관리한계선을 어떻게 설정하여야 공정이 정상일 때는 밖으로 나가지 않고, 공정에 이상이 있을 때는 즉시 이 선을 벗어나도록 할 것인가로 요약됨

공정이 정상일 때는 한계선 밖으로 나가 오경종(false alarm)을 울리는 오류(이를 1종 오류 또는 생산자에 손실을 입히므로 생산자 위험이라고 함)가 적어야 하며 동시에 공정 상 이상이 발생했음에도 불구하고 경종을 울리지 않는 오류(이를 2종 오류 또는 소비자 위험이라고 함) 또한 적어야 함

이 두 가지를 만족시키는 관리도를 설계하기란 쉬운 일이 아니지만 3-시그마 규칙에 의거한 관리한계선 설정이 비교적 잘 만족시켜주며 따라서 널리 사용되고 있음

품질특성을 반영하는 표본통계량을 $W$라 하고 W의 평균 및 표준편차를 각각 $\mu_W$, $\sigma_W$라 할 때, 관리도의 중심선 및 3-시그마 규칙에 의한 관리한계선은 다음과 같음

$$\tag{13.1} \begin{cases} UCL = \mu_W + 3\sigma_W \\ CL = \mu_W \\ LCL = \mu_W - 3\sigma_W \end{cases}$$

여기서 $\mu_W, \sigma_W$는 통상 모르는 값이므로 데이터로부터 추정하여야 함

관리한계선 설정에는 경영자의 의지가 반영될수도 있음

나쁜 품질이 소비자에 미치는 영향을 크게 고려한다면 조금 잦은 오경종을 무릅쓰고라도 관리한계선을 좁혀 소비자 위험을 줄일수도 있음

또한 두 가지 오류(위험)에 대한 비용을 산출할 수 있다면 총 비용이 가장 적게 되도록 하는 관리도의 경제적 설계로 고려 가능

대표적인 계량형 관리도인 $\bar X$관리도에서의 관리한계선 설정

어느 한 시점에서 품질 특성치를 관리도에 표시할 때 공정에서 여러 개의 표본을 추출하여 각 특성치를 측정하고 그 평균치를 기록

따라서 $X$관리도라 하지않고 $\bar X$관리도라고 함

여기서 한번에 추출하는 표본들을 하나의 부분군(subgroup)이라고 함

중요한 사실은 이렇게 여러 표본의 평균치를 택하므로 비록 개개의 표본 측정치($X$)는 정규분포를 따르지 않더라도 그 평균치($\bar X$)는 표본크기가 커질수록 정규분포에 근사하게 됨 (중심극한정리에 의거)

하지만 표본크기(부분군의 크기)를 너무크게하면 평균을 취함으로써 표본 내에 있을 수 있는 변동이 서로 상쇄되어 실제 공정에 있었을 어떤 변화를 알 수 없을 뿐더러 비용도 많이 들기 때문에 실제로는 '적당한' 수를 택해야 함

통상 4~5개가 추천도고 있으며 이정도로도 그 평균치는 정규분포에서 크게 벗어나지 않음

표본추출비용이 극히 크거나 액체와 같이 균일한 제품에서는 1개의 표본을 이용하기도 함 (이 경우 X관리도라고 함)

평균을 취함으로써 얻는 이득 중 하나는 불필요한 변동이 상쇄되어 적어진다는 것

표본평균($\bar X$)의 표준편차는 표본크기의 제곱근에 반비례하게 되는데, 예를 들어 공정의 표준편차(각 표본의 표준편차)가 $\sigma$일 때, 4개의 표본을 택하여 평균한 $\bar X$의 표준편차 ($\bar X$의 표준편차를 $\sigma_{\bar X}$로 표시)는 $\sigma /\sqrt{4} = \sigma /2$이므로 $\bar X$의 변동은 원래 공정보다 반으로 줄어듬

표본크기가 클수록 $\bar X$의 변동은 이와 같이 줄어들어 공정이 정상일 때 $\bar X$를 관리도에 표시하면 그 경향이 부드럽게 상하로 움직이게 됨

공정에 이상이 발생할 때는 급격하게 변화하므로 공정의 이상을 쉽게 관찰할 수 있는 이점도 있음

식 13.1에 의한 3-시그마 관리한계선을 표현하면 $\bar X$관리도의 경우 $W$에 해당하는 통계량이 $\bar X$이므로 다음과 같음

$$\tag{13.2} \begin{cases} UCL = \mu_{\bar X} + 3\sigma_{\bar X} \\ CL = \mu_{\bar X} \\ LCL = \mu_{\bar X} - 3\sigma_{\bar X} \end{cases}$$

식 13.2에서 $\mu_{\bar X} = \mu$이며 $\sigma_{\bar X} = \sigma/\sqrt{n}$인데, 공정의 실제 평균 $\mu$와 실제 표준편차 $\sigma$는 모르는 값

이 값들을 추정하기 위해서는 시간 경과에 따른 다수의 부분군으로부터 $\bar X$값들이 준비되어야 함

이 때 공정평균 $\mu$는 여러 $\bar X$들의 평균인 $\bar{\bar X}$로 추정할 수 있고, 공정 표준편차 $\sigma$는 흔히 간편한 방법으로 각 부분군에서 범위(각 부분군에서 가장 큰 값에서 가장 작은 값을 뺀 것으로 R로 표시) 로 추정 $\Rarr$ 범위도 공정의 변동을 대표하고 있기 때문

범위를 이용하는 또 하나의 이유는 보통 $\bar X$관리도와 동시에 범위를 관리하는 R관리도를 함께 그리기 때문

13.1.2 관리상태 여부의 판정

위와 같은 원리에 의해 관리한계선이 설정되면 계속적으로 같은 크기의 표본을 정기적으로 추출하여 적절한 통계량 ($\bar X$관리도의 경우 $\bar X$)을 기록함으로써 공정을 관측

관리한계선을 벗어나는 점이 있을 때는 공정에 이상이 있다고 선언하며 실제 이상 여부를 조사해야 함

모든 점이 관리한계선 내에 있을지라도 관리도 상에 '특이한' 현상이 있을 경우는 공정이 정상이 아니라고 의심할 수 있음

예를 들어 관리한계선 부근에 자주 기록된다거나 연속된 7개 이상의 점이 중심선 위 또는 아래 한 쪽에 나타나는 경우를 말함

$\Rarr$ 공정이 정상인 경우 중심선 부근에 많은 점들이 오게 되어 있으며 중심에서 멀리 떨어져 있는 경우는 적기 때문

관리도에서 $2\sigma$와 $3\sigma$사이에 어떤 한 점이 있을 확률은 약 0.0214이므로 연속한 두 점이 $2\sigma$와 $3\sigma$ 사이에 있을 확률은 $(0.0214)^2 = 0.00046$으로 상당히 작으므로 이 경우 공정의 이상을 의미할 수 있음

관리한계선을 벗어난 점이 없더라도 다음과 같은 현상이 나타나면 공정이 관리 상태를 이탈했을 가능성이 있다고 봄

💡

1. 연속 7점 이상이 중심선의 어느 한쪽에만 계속될 때 2. 연속 11점 중 10점 이상이 중심선의 어느 한 쪽에 위치할 때 3. 연속 14점 중 12점 이상이 중심선의 어느 한 쪽에 위치할 때 4. 연속 7점 이상이 계속하여 상승 또는 하강할 때 5. 연속 3점 중 2점 이상이 $2\sigma$ 한계선을 넘을 때 6. 연속 5점 중 4점 이상이 $1\sigma$ 한계선을 넘을 때 7. 어떤 경향이나 주기성을 나타낼 때

13.1.3 관리도의 종류

관리도는 제품의 품질특성에 따라 크게 계량형 관리도와 계수형 관리도로 분류

일반적으로 널리 사용되는 계량형 및 계수형 관리도는 다음과 같음

(1) 계량형 관리도(charts for variables)

1. 공정평균 관리용 : $X$ 관리도, $\bar X$관리도, 누적합 (cumulative sum; CUSUM) 관리도, 이동평균 (moving average) 관리도, 지수가중 이동평균(exponentially weighted moving average: EWMA) 관리도

2. 공정산포 관리용 : $R$ 관리도, $s$ 관리도, $s^2$ 관리도

(2) 계수형 관리도(charts for attributes)

1. 불량률 관리용 : $p$ 관리도, $np$ 관리도

2. 결점수 관리용: $c$ 관리도, $u$ 관리도

누적합 관리도, 이동평균 관리도, 지수가중 이동평균 관리도 등은 슈하르트 이후에 개발된 것\

사용법은 약간 복잡하지만 슈하르트 관리도보다 대체로 효율적인 것으로 알려져 있음

13.2 계량형 관리도

제품의 품질특성이 길이, 중량, 강도, 부피 등과 같이 연속적으로 변하는 수치를 갖는 경우를 계량형 품질특성이라고 함

품질특성이 계량형인 경우 공정의 평균 및 산포가 직접 품질에 영향을 미치므로 평균과 산포를 모두 관리할 필요가 있음

공정평균의 관리를 위해서는 $\bar X$ 또는 $X$ 관리도 사용

공정 산포의 관리를 위해서는 $R$ 또는 $s$ 관리도 사용

13.2.1 $\bar X-R$ 관리도

공정 평균의 관리를 위해 $\bar X$관리도, 공정 표준편차의 관리를 위해 범위를 이용한 $R$ 관리도를 적용하는 경우 이를 묶어서 $\bar X - R$관리도라고 함

$X_1, X_2, \dots, X_n$을 평균이 $\mu$, 표준편차가 $\sigma$인 정규모집단으로부터 추출한 크기 $n$인 하나의 부분군에 대한 표본이라 할 때 $\bar X$관리도는 매번 부분군별로 표본평균인 $\bar X$를 타점하는 것

표본평균 $\bar X$는 평균이 $\mu$, 표준편차가 $\sigma/\sqrt{n}$을 따름

따라서 $\mu, \sigma$를 알고 있는 경우 중심선 및 3-시그마 관리한계선은 식 13.1 또는 식 13.2에 의해 다음과 같이 구해짐

$$\tag{13.3} \begin{cases} UCL = \mu + \frac{3\sigma}{\sqrt{n}} \\ CL = \mu \\ LCL = \mu - \frac{3\sigma}{\sqrt{n}} \end{cases}$$

만약, $\mu, \sigma$를 모르는 경우에는 예비표본으로부터 추정한 값을 이용하여 관리한계선을 구할 수 있음

관리상태의 공정으로부터 크기 $n$의 부분군을 시간에 따라 $m$개 마련하는 경우 ($m$값으로는 보통 20 이상의 값을 사용)

$\bar X_i, R_i\;(i=1,2,\dots, m)$을 각각 i번째 부분군의 평균 및 범위라 할 때 이들의 전체 평균은 각각 다음과 같이 주어짐

$$\bar {\bar X} = (\bar X_1 + \bar X_2 + \dots + \bar X_m)/m \\ \bar R = (\bar R_1 + \bar R_2 + \dots + \bar R_m)/m$$

위의 자료들로부터 $\mu$의 불편추정량을 구하면 다음과 같음

$$\tag{13.4} \hat \mu = \bar{\bar X}$$

$\sigma$는 범위 $R$의 기대치와 $\sigma$와의 다음과 같은 관계를 이용하여 추정

$$E[R] = d_2 \sigma$$

여기서 d_2는 n에 따라 다른 상수로써 표 13.1과 같은 값을 가짐 (정규분포표처럼 정리되어있음)

$n$	2	3	4	5	6	7	8
$d_2$	1.128	1.693	2.059	2.326	2.534	2.704	2.847

따라서 $E[R]$을 예비표본의 $\bar R$로 추정하면 $\sigma$는 다음과 같이 추정됨

$$\tag{13.5} \hat \sigma = \frac{\bar R}{d_2}$$

$\mu$의 추정치로 $\bar{\bar X}, \sigma$의 추정치로 $\bar R/d_2$를 이용하여 식 13.3에 의한 $\bar X$관리도의 중심선 및 3-시그마 관리한계선을 구하면 다음과 같다

$$\tag{13.6} \begin{cases} UCL = \bar{\bar X} + (\frac{3\sigma}{\sqrt{n}})(\frac{\bar R}{d_2})=\bar{\bar X} + A_2R \\ CL = \bar{\bar X}\\ LCL = \bar{\bar X} - (\frac{3\sigma}{\sqrt{n}})(\frac{\bar R}{d_2})=\bar{\bar X} - A_2R \end{cases}$$

여기서$A_2 = \frac{3}{d_2\sqrt{n}}$으로 $n$에 따라 미리 계산되는 값

$X$관리도는 부분군의 크기 n이 1인 경우로 범위를 구할 수 없기 때문에 이동범위 (moving average)를 구함

즉 바로 전 관측치와의 범위를 구하여 평균범위를 구한 후 식 13.5를 이용하여 $\sigma$를 추정 ($d_2 = 1.128$ 사용)

$X$관리도의 경우에도 식 13.6을 사용할 수 있으며 $A_2 = 2.6596$ 사용

표본범위 $R$은 공정의 표준편차와 관련이 있음

$R$관리도는 공정의 산포를 관리하기 위해 매시점 부분군의 $R$을 플롯하는 것

$R$관리도의 관리한계선을 구하기 위해선 $R$의 기대치와 표준편차를 알아야하는데 이는 다음과 같이 주어짐

$$\begin{aligned} \mu_R &= E[R] = d_2\sigma \\ \sigma_R &= \sqrt{Var[R]} = d_3\sigma \end{aligned}$$

따라서 $\sigma$를 알고 있는 경우 R관리도의 중심선 및 3-시그마 관리한계선은 다음과 같다

$$\tag{13.7} \begin{cases} UCL = \mu_R+3\sigma_R = (d_2 + 3d_3)\sigma=D_2\sigma \\ CL = \mu_R=d_2\sigma\\ LCL = \mu_R-3\sigma_R = (d_2 - 3d_3)\sigma=D_1\sigma \end{cases}$$

$\sigma$를 모르는 경우 추정치 $\hat \sigma = \bar R/d_2$를 이용하여 다음과 같이 계산 가능

$$\tag{13.8} \begin{cases} UCL = \bar R + 3d_3\bar R/d_2 = D_4\bar R \\ CL = \bar R \\ LCL = \bar R - 3d_3\bar R/d_2 = D_3\bar R \end{cases}$$

$\bar X - R$관리도 예시

관리도 타점 시 관리한계선을 벗어나는 점이 있다면 해당 부분군의 데이터를 제거 후 관리한계선을 다시 설정하는 것이 바람직

관리한계선을 설정하기 위해서는 정상인 공정으로부터 예비표본을 추출하여야 하기 때문

13.2.2 $s$ 관리도

$s$ 관리도는 $R$ 관리도와 같이 공정산포를 관리하고자 하는 것

매 시점에 $n$ 개의 크기를 갖는 부분군 별로 표준편차 $s$를 산출하여 플롯하는 것

대체로 부분군 크기 $n$이 클 때 (약 10 이상) $R$ 관리도보다 효율적인 것으로 알려져 있음

$s$는 $\sigma$의 불편추정량은 아니며 기대치와 표준편차는 다음과 같이 산출됨

$$\begin{aligned} \mu_s &= E[s] = c_4\sigma \\ \sigma_s &= \sqrt{Var[s]} = \sqrt{1-c_4^2} \;\cdot \;\sigma \end{aligned}$$

여기서 $c_4$는 $s$를 $\sigma$의 불편추정량으로 바꾸어 주는 상수

$n$에 값에 따라 변하는 값을 가지며 미리 계산되어 있음

$\sigma$를 안다고 할 때 $s$ 관리도의 관리한계선은 다음과 같음

$$\tag{13.9} \begin{cases} UCL = \mu_s + 3\sigma_s = c_4\sigma + 3\sqrt{1 - c_4^2} \;\cdot\; = B_6\sigma \\ CL = \mu_s = c_4\sigma \\ LCL = \mu_s - 3\sigma_s = c_4\sigma - 3\sqrt{1 - c_4^2} \;\cdot\; = B_5\sigma \end{cases}$$

$B_6 = c_4 + 3\sqrt{1-c_4^2}, \; B_5 = c_4 - 3\sqrt{1-c_4^2}$ 으로 미리 계산되어져 있음

$\sigma$를 모를 경우 $m$ 개의 예비 부분군으로부터 다음과 같이 $\bar s$를 산출한 후

$$\bar s = (s_1 + s_2 + \dots + s_m) / m$$

$\sigma$를 아래와 같이 추정

$$\tag{13.10} \hat \sigma = \frac{\bar s}{c_4}$$

식 13.9의 $\sigma$ 대신 식 13.10의 $\hat \sigma$ 를 대입하면 관리한계선은 다음과 같다

$$\tag{13.11} \begin{cases} UCL = \bar s + 3\sqrt{1-c_4^2} (\frac{\bar s}{c_4}) = B_4\bar s \\ CL = \bar s \\ LCL = \bar s - 3\sqrt{1-c_4^2} (\frac{\bar s}{c_4}) = B_3\bar s \end{cases}$$

13.3 계수형 관리도

13.3.1 불량률 관리도(관리도)

불량률이 p인 생산공정으로부터 크기 n인 표본을 취해 그 중에서 발견되는 불량품수를 $X$라 할 때, $X$는 이항분포 $Bin(n,p)$를 따르고 평균과 분산은 각각 $np, \; np(1-p)$

불량률을 관리하는 $p$ 관리도는 추출되는 부분군의 불량률 $\hat p = X/n$을 타점

$\hat p$의 기대치와 분산은 아래와 같다

$$\begin{aligned} E[\hat p] & E\left[\frac{X}{n}\right] = \frac{np}{n} = p \\ Var[\hat p] &= Var\left[\frac{X}{n}\right] = \frac{np(1-p)}{n^2} = \frac{p(1-p)}{n} \end{aligned}$$

$p$ 관리도의 3-시그마 관리한계선은 각각 다음과 같이 구할 수 있음

$$\tag{13.12} \begin{cases} UCL = p + 3\sqrt{p(1-p)/n} \\ CL = p \\ LCL = p - 3\sqrt{p(1-p)/n} \end{cases}$$

공정불량률 $p$를 모를 경우에는 일정기간동안 관측된 자료로부터 $p$를 추정하여 사용

$p$를 추정하기 위해서는 보통 20개 이상의 예비 부분군을 추출하여 사용

$i$번째 부분군의 크기 및 부분군 내 불량수를 각각 $n_i, X_i$라 할 때 $m$번의 예비 부분군으로부터 추정된 평균불량률 $\bar p$는 다음과 같다

$$\bar p = \frac{총불량품수}{총검사개수} = \frac{\sum_{i=1}^n X_i}{\sum_{i=1}^m n_i}$$

이를 식 13.12에 대입하여 $p$관리도의 중심선 및 관리한계선을 구하면 다음과 같다

$$\tag{13.13} \begin{cases} UCL = \bar p + 3\sqrt{\bar p(1-\bar p)/n} \\ CL = \bar p \\ LCL = \bar p - 3\sqrt{\bar p(1-\bar p)/n} \end{cases}$$

부분군의 크기가 표본시마다 다른 경우에는 관리한계선이 매번 달라짐

$i$번째 부분군의 크기를 $n_i$라 하면 이에 대응하는 관리한계선은 다음과 같다

$$\tag{13.14} \begin{cases} UCL = \bar p + 3\sqrt{\bar p(1-\bar p)/n_i} \\ CL = \bar p \\ LCL = \bar p - 3\sqrt{\bar p(1-\bar p)/n_i} \end{cases}$$

여기서 LCL값이 음수이면 0으로 둠

불량률 대신 직접 불량개수를 타점하여 관리하는 것을 불량개수관리도 또는 $np$ 관리도라고 함

13.3.2 결점수관리도

하나의 제품에 약간의 결점만 있으면 불량으로 처리되지 않고 사용 가능한 경우가 있음

예를 들어 전선, 직물, 두루마리 종이제품 등의 경우, 일정한 길이 또는 면적 당 약간의 흠이 있어도 실제 사용에는 지장 없음

그러나 결점의 수가 많아지면 제품의 기능이 저하되거나 가치가 감소

이와 같은 제품 당 결점수를 관리하기 위해 고안된 관리도가 결점수관리도

결점수관리도에서는 제품 당 결점수 $X$가 포아송분포를 따른다고 가정

$X$가 평균 $c$인 포아송분포를 따를 때 $X$의 평균과 분산은 모두 $c$

편의 상 제품 당 결점수라는 표현을 사용하지만 반드시 한 제품에 대한 결점수인 것은 아님

5개 제품에 대한 결점수를 집계하는 경우 5개 제품을 하나의 부분군으로 관리할 수도 있음

관리하는 검사 단위에 대한 결점수를 다루는 관리도를 $c$ 관리도라고 하며, 단위당 결점수를 다루는 경우 $u$ 관리도라고 함

(1) c 관리도(결점수 관리도)

$c$ 관리도는 결점수 $X$를 타점하는 것으로 $X$의 기대치와 분산이 동일하게 $c$

3-시그마 관리한계선은 다음과 같다

$$\tag{13.15} \begin{cases} UCL = c + 3\sqrt{c} \\ CL = c \\ LCL = c - 3\sqrt{c} \end{cases}$$

LCL값이 음이 될 때는 0으로 둠

$c$값을 모르는 경우 다음과 같이 예비샘플로부터 추정하여 사용

$$\bar c = \frac{발견된\;총결점수}{총부분군수}$$

(2) $u$ 관리도(단위당 결점수관리도)

결점수관리도에서 공정변화의 감지능력(민감도)나 경제적 요인들을 고려하여 여러 개의 검사 단위를 묶어서 하나의 부분군 형성 가능

이 때 하나의 부분군을 이루는 검사단위수를 $k$라 하면 검사단위당 결점수 $U=X/k$의 기대치와 분산은 다음과 같다

$$E[U] = E\left[\frac{X}{k}\right] = \frac{c}{k} \\ Var[U] = Var \left[\frac{X}{k}\right] = \frac{c}{k^2}$$

$u$관리도에서는 검사단위당 결점수 $U$를 타점

$U$의 기대치를 $u=c/k$라 하면 $u$관리도의 3-시그마 관리한계선은 다음과 같다

$$\tag{13.16} \begin{cases} UCL = u + 3\sqrt{u/k} \\ CL = u \\ LCL = u - 3\sqrt{u/k} \end{cases}$$

$u$값을 모를 때는 다음과 같이 예비샘플로부터 추정한 값 $\bar u$를 사용

$$\bar u = \frac{발견된\;총결점수}{총검사\;단위수}$$

$u$관리도에서 부분군별로 검사단위가 다를 수 있는데 $i$번째 부분군의 검사 단위가 $k_i$ 일 때 관리한계선은 식 13.16에서 $k$대신 $k_i$를 대입하면 됨

이 때 관리한계선은 부분군마다 변하게 됨

13.4 관리도의 공정변화 감지능력

공정의 관리상태 여부를 탐지할 목적으로 관리도를 사용하는 경우 관리도가 공정변화에 얼마나 민감한지 알아볼 필요가 있음

검사특성곡선 또는 OC(operating characteristic curve)곡선은 공정품질수준이 변화한 직후 관리도 상에 타점한 한 점이 관리한계선 내에 들어감으로써 공정에 변화가 없다고 잘못 판단할 확률(소비자 위험)을 공정변화의 함수로 나타낸 것

$\bar X$ 관리도에 대한 OC곡선의 경우 공정품질이 평균 $\mu$, 분산 $\sigma^2$의 정규분포를 따른다고 하고 식 13.3의 관리한계선을 가지는 $\bar X$관리도를 사용한다고 할 때, 어느 시점에서 공정분산은 그대로 유지되면서 공정평균이 다음과 같이 $\sigma$의 $k$배만큼 증가한다고 가정

$$\tag{13.17} 공정평균변화:\;\mu \rarr \mu + k\sigma$$

공정변화 직후 타점한 $\bar X$가 여전히 관리한계선($\mu \pm 3\sigma/\sqrt{n}$)내에 있어 공정변화를 감지하지 못할 확률은 다음과 같다

$$\beta = P\{LCL \leq \bar X \leq UCL \; |\;공정평균=\mu + k\sigma\}$$

따라서 확률 $\beta$는 다음과 같이 구할 수 있다

$$\tag{13.18} \begin{aligned} \beta &= P \left\{\mu - \frac{3\sigma}{\sqrt{n}} \leq \bar X \leq \mu + \frac{3\sigma}{\sqrt{n}}\;|공정평균=\mu +3\sigma\right\} \\ &= P \left\{ \frac{\mu - 3\sigma/\sqrt{n} - (\mu+k\sigma)}{\sigma/\sqrt{n}} \leq \frac{\bar X - (\mu+k\sigma)}{\sigma/\sqrt{n}} \leq \frac{\mu + 3\sigma/\sqrt{n} - (\mu+k\sigma)}{\sigma/\sqrt{n}} \right\} \\ &= P\{-3-k/\sqrt{n} \leq Z \leq 3-k\sqrt{n}\} \\ &= \Phi(3-k\sqrt{n}) - \Phi(-3-k\sqrt{n}) \end{aligned}$$

여기서 $\Phi(\cdot)$은 표준정규분포를 따르는 Z의 누적분포함수로써 표준정규분포를 이용하여 다음과 같이 구할 수 있다

$$\Phi(z) = 1 - P\{Z > z\}$$

공정변화를 감지할 확률은 $1-\beta$임을 알 수 있음

식 13.18의 확률 $\beta$를 $k$에 대한 함수로 나타낸 것을 OC곡선이라 함

다른 관리도에 대해서도 유사하게 확률 $\beta$를 구할 수 있으며 OC 곡선을 그릴 수 있음

공정변화가 작은 경우에는 한번에 그 변화를 감지하기는 어려움 따라서 공정변화 후 관리도 상에 몇 번째 타점 후 감지할 수 있는가에 관심을 가짐

한 점으로 감지할 확률이 $1-\beta$이므로 정확히 j번째 점에서 감지할 확률은 다음과 같다 즉, 감지할 때까지 걸리는 시간(타점수)을 $L$이라 하면 $L = j$일 확률은 아래와 같다

$$\tag{13.19} P\{L = j\} = \beta^{j-1}(1-\beta),\;j=1,2,\dots$$

위와 같은 확률밀도함수를 갖는 L과 같은 확률변수는 기하분포 (geometric distribution)을 따름 감지할 때까지 걸리는 시간의 기대치를 평균런길이 (average run length; ARL)이라고 함

ARL은 관리도의 공정변화 감지능력의 척도로 사용됨 따라서 ARL은 위의 분포를 가지는 L의 기대치이며 다음과 같다

$$\tag{13.20} ARL = E[L] = \sum^\infin_{j=1}j\beta^{j-1}(1-\beta) = \frac{1}{1-\beta}$$

13.5 공정능력분석

통계적 품질관리의 주요 기능 중 하나는 공정을 관리상태로 유지하는 것

그 공정으로부터 생산된 제품들이 규격을 만족하도록 공정을 유도 및 조정하는 일 또한 중요

생산된 제품들이 '얼마나 규격을 만족하는가' 그렇지 못하다면 '규격을 만족하도록 공정을 조정할 수는 없는가' 하는 문제들이 공정능력분석의 영역에 해당

💡

공정설계 및 제조단계에서 생산공정의 품질 변동 정도를 측정하고 규격과 비교 분석하는 것을 공정능력분석(process capability analysis) 이라 함

공정능력이란 생산공정이 얼마나 균일한 품질의 제품을 생산할 수 있는지를 반영하는 공정의 고유 능력을 의미로 척도로는 일반적으로 $6\sigma(\pm3\sigma)$를 사용

제품의 품질특성이 정규분포를 따르는 경우 거의 대부분(99.73%)이 평균을 중심으로 이 범위에 포함되기 때문

규격과 관련하여 공정능력을 평가하는 척도로서 공정능력지수(process capability index)가 있음 $(C_p,\;C_{pk})$

공정능력지수는 공정능력($6\sigma$)에 대한 규격폭의 비율로서 공정이 규격에 맞는 제품을 생산할 능력을 가지고 있는지를 나타내는 지수

규격상한 (upper specification limit; USL)과 규격하한 (lower specification limit; LSL)이 주어진 경우 공정능력지수 $C_p$는 다음과 같이 정의

$$\tag{13.21} C_p = \frac{USL - LSL}{6\sigma}$$

$C_p = 1$인 경우 규격폭(=USL - LSL)이 $6\sigma$와 일치하는 경우로 이런 공정하에서 규격을 벗어날 확률이 0.0027

따라서 불량률을 이보다 작게하기 위해서는 동일한 규격 하에서 $\sigma$를 줄여야 함

$C_p = 1.5$이상으로 한다는 것은 규격폭을 공정능력의 1.5배 이상으로 하여야 한다는 것을 뜻함

공정의 $\sigma$를 규격폭의 1/9이하로 하여 불량률을 백만분의 6.8, 즉 6.8ppm 이하로 하여야 함을 의미

USL 또는 LSL 한쪽 규격만 주어지는 경우 공정능력지수는 다음과 같이 정의됨

$$\tag{13.22} C_p = \begin{cases} \frac{(USL - \mu)}{3\sigma} \;\;USL만\;있는\;경우 \\ \frac{(\mu-LSL)}{3\sigma} \;\;LSL만\;있는\;경우 \end{cases}$$

식 13.22의 $C_p$는 공정의 평균을 고려하지 않았으나 이를 고려한 것이 $C_{pk}$지수 $C_{pk}$지수는 다음과 같이 정의됨

$$\tag{13.23} C_{pk} = \frac{min[USL - \mu, \mu - LSL]}{3\sigma}$$

따라서 공정평균 $\mu$가 양쪽규격의 한 가운데에 위치하게 되면 두 지수는 일치

그러나 어느 한 쪽으로 치우친 경우에는 $C_{pk}$가 $C_p$보다 작게 됨

13.6 샘플링검사

안전면이나 경제적인 이유에서 어느 정도 불량을 허용할 수 있는 경우에 전수 검사의 수고와 시간, 비용을 줄이기 위해 로트로부터 일부를 무작위로 채취하여 검사하는 것을 샘플링 검사라고 함

샘플링검사는 다시 계수샘플링검사 (sampling inspection by attributes)와 계량샘플링검사 (sampling inspection by variables)로 구분

계수샘플링검사는 검사단위의 품질이 불량품수, 불량률 또는 결점수 등으로 표시되는 경우

계량샘플링검사는 품질이 길이, 중량, 강도 등과 같이 측정가능한 계량치로 표시되는 경우

이 중에서는 주로 계수샘플링검사가 많이 사용됨

공정에서 제품이 로트 (lot) 단위로 생산된다고 할 때 한 로트에 제품이 N개씩 있다고 할 때 위에서 언급한 바와 같이 어떤 로트에는 '많은' 불량품이 들어있을 수 있기 때문에 이러한 불량이 소비자에게 전해지는 것을 최대한 방지하고자 검사를 실행하게 됨

각 로트에 대해 100% 전량을 검사하는 것을 전수검사 (screening)이라고 함

전수검사는 주로 한 로트에 소량의 값비싼 제품을 포함하고 있으며 불량품이 하나라도 있는 경우 불이익이 큰 경우 시행

많은 시간과 비용이 소요되므로 주로 무작위 추출하여 검사하는 샘플링 검사를 주로 시행

13.6.1 계수샘플링검사의 종류

샘플링검사 방안에는 여러 가지가 있음

기본적으로는 한 로트에서 '적당한' 수의 표본을 추출하여 불량품 수가 어느 수준 이하이면 그 로트를 합격시키고 어느 수준보다 많으면 그 로트를 폐기하려는 것

따라서 몇 개의 표본을 선택해야 하며 합격, 불합격 판정 수준을 어떻게 정할 것인가가 주 관심사 여기에는 표본검사방안과 밀접한 관계가 있느 검사특성곡선 (operating characteristic curve; OC curve)에 대해 알아야 함

먼저 기본적인 샘플링검사의 종류는 다음과 같다

(1) 1회 샘플링검사

1회 샘플링검사는 1회의 샘플링으로 로트에 대한 합/불 판정을 내리는 샘플링검사 n개의 표본을 채취하여 이 중 불량품수가 c개 이하이면 로트 합격, 그보다 많으면 불합격 즉 1회 샘플링검사의 모수는 $(n, c) \rarr c$를 합격판정개수 (acceptance number) 라 함

불량품수를 $X$라 할 때 1회 샘플링검사를 통해 불량률이 p인 로트가 합격할 확률은 다음과 같다

$$\tag{13.24} P_a = P\{X \leq c\} = \sum_{x=0}^c\frac{n!}{x!(n-x)!}p^x(1-p)^{n-x}$$

(2) 2회 샘플링검사

1차 표본검사에서 표본수 $n_1$개를 추출하여 불량품수가 $c_1$이하이면 로트를 합격시키고 $r_1$개 이상이면 불합격판정 (합격, 불합격이 확실한 경우)

그 중간의 결과에 대해서는 2차로 표본 $n_2$개를 검사하여 2회 표본에 대한 불량품 합계가 $c_2$ 이하이면 합격하고 그렇지 않으면 불합격

2회 샘플링검사의 모수는 $(n_1, n_2, c_1, r_1, c_2)$

1차 표본에서의 ($n_1$ 개 중) 불량품수를 $X_1$이라하고 2차 표본에서의 ($n_2$ 개 중) 불량품수를 $X_2$라 할 때 불량률이 $p$ 인 로트를 합격시킬 확률은 다음과 같다

$$\tag{13.25} P_a = P\{X_1 \leq c_1\} + P\{c_1 < X_1 < r_1, \; X_1 + X_2 \leq c_2\}$$

위 식에서 첫 항은 1차에서 합격시킬 확률

두 번째 항은 1차에서 결정나지 않았다가 2차에서 합격할 확률

2회 샘플링검사를 동일한 로트 불량률과 합격확률 하에서 1회 샘플링검사와 비교할 때 2회 샘플링검사의 소요되는 평균검사수(average sample number; ASN)이 더 작음을 이론적으로 밝힐 수 있어 비용면에서는 더 유리할 것으로 예상됨

하지만 복잡성으로 실제는 사용빈도가 적음

또한 2회 샘플링검사를 확장하여 다회 샘플링검사 (mutiple sampling plan)을 고려할 수도 있음

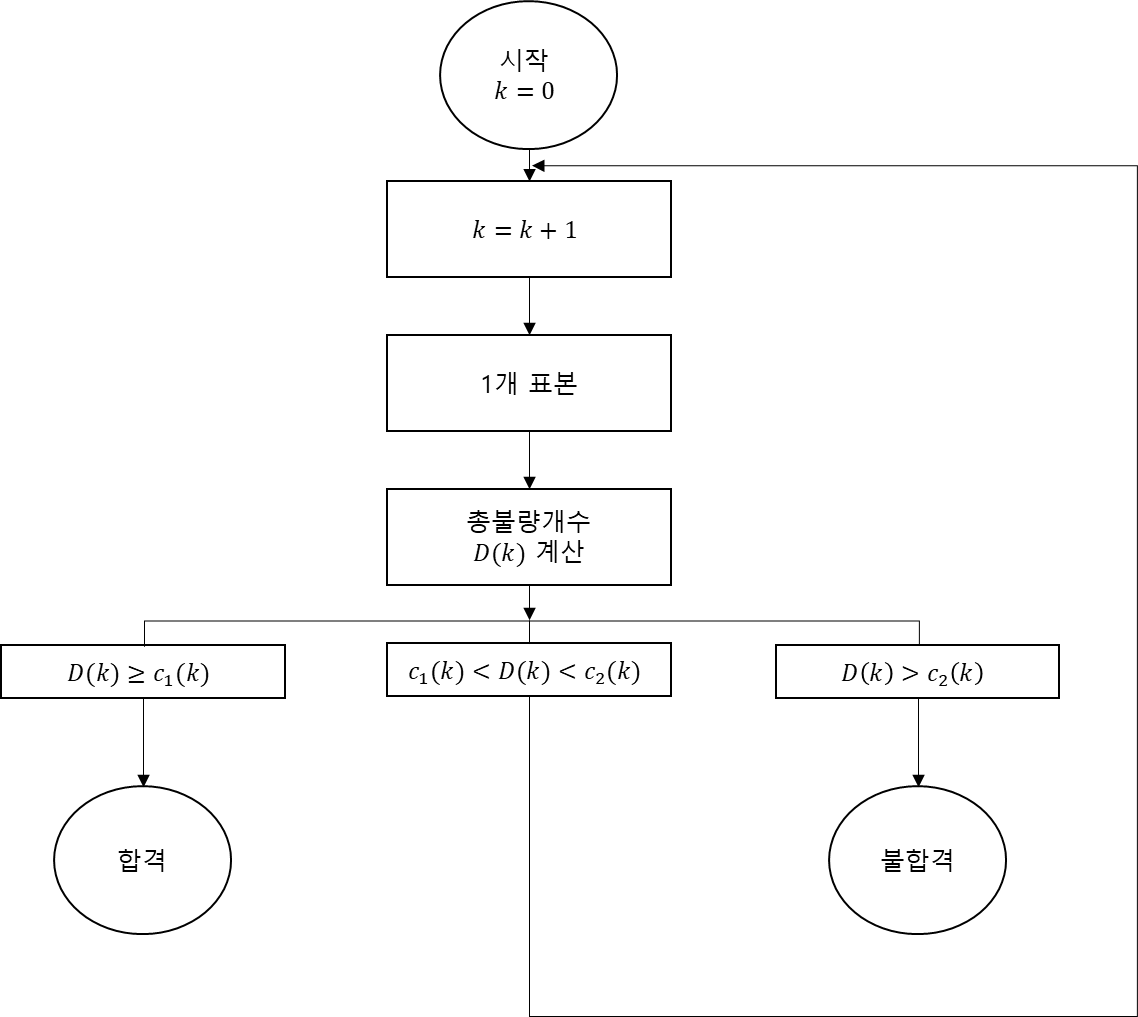
(3) 축차샘플링검사

파괴검사와 같이 표본수를 최소로 하는 것이 대한히 중요한 경우에는 축차샘플링검사 (sequential sampling plan)을 사용하기도 함

한번에 한 제품씩 추출하여 $k$시점에서 총 불량품수 $D(k)$가 $c_1(k)$ 이하이면 로트를 합격시키고 $c_2(k)$ 이상이면 불합격시키며 그 중간이면 다시 한 표본을 추출하여 과정을 반복하는 방법

여기서 언급한 샘플링검사방안 외에도 많은 방안들이 있음

샘플링검사가 적극적으로 품질을 개선하는 것은 아니라 할 지라도 불량률을 줄일 수 있는 최후의 수단이므로 간과할 수 없음

13.6.2 로트합격확률 및 OC 곡선

로트의 불량률을 로트크기 $N$에 대한 로트에 포함되어 있는 불량품개수의 비율로 정의하고 $p$로 표시한다고 하면 불량률 $p$값을 모르는 것이 보통

한 로트에 들어 있는 불량품 개수는 전수검사를 하지 않는 이상 모르기 때문, 만약 p값을 안다면 표본검사를 할 필요가 없음

불량률을 모르기 때문에 어떠한 표본검사방안을 채택한다고 하더라도 좋은 로트를 불합격시킬 수도 있고 나쁜 로트를 합격시킬수도 있음

불량률 $p$가 어떤 고정된 값을 가질 때 채택하고 있는 샘플림검사방안에 따른 로트의 합격 확률 $P_a$를 식 13.24, 13.25 등과 같이 구할 수 있음 $p$값을 x축으로 $P_a$값을 y축으로 하여 그래프로 나타낸 곡선을 검사특성곡선 또는 OC곡선이라고 함

바람직한 OC 곡선의 모양은 전수검사의 경우와 같이 불량률이 어느 수준 ($p_s$)보다 작으면 합격확률이 1이고 이보다 클 때 0이 되는 형태가 바람직

샘플링검사에는 실제 불량률을 알 수 없기 때문에 이러한 오류가 발생하게 됨

즉 샘플링검사의 경우에는 실제 p값이 작다고 하더라도 로트가 불합격될 확률이 존재하여 합격확률 $P_a$가 1에 가깝긴 하지만 정확히 1은 아님

$p$ 값이 큰 경우에도 합격확률이 존재하여 정확히 0이 되지는 않음

OC 곡선은 주어진 샘플링검사 방안에 대해 여러 $p$값 (0에서 1사이의 연속된 값)에 따라 로트합격확률을 한눈에 볼 수 있도록 나타낸 것

실제 OC곡선을 그리려면 어떤 주어진 $p$값에 대해 합격확률 $P_a$를 계산해야함 합격확률은 샘플링검사방안에 의해 좌우됨

1회 샘플링검사의 경우 식 13.24에 의해 산출될 수 있음

$$P_a = \sum_{i=1}^c \begin{pmatrix}n\\i\end{pmatrix}p^i(1-p)^{n-i}$$

표본크기 $n$이 크고 불량률 $p$가 작으면 이항분포는 다시 포아송분포에 근사하게 되어 $\theta = np$ 라고 할 때 다음과 같이 계산할 수 있다

$$P_a = \sum_{i=0}^c \frac{e^{-0}\theta^i}{i!}$$

따라서 포아송 근사식에 따르면 주어진 p값에 대해 $\theta$ 값을 계산하고 로트합격확률을 비교적 손쉽게 구할 수 있음

13.6.3 1회 샘플링검사의 설계

1회 샘플링검사는 한번에 '적당한' 표본수를 택하여 로트의 합격여부를 판정하는 방법으로 과연 몇 개의 표본을 택해야 하며 몇 개의 불량품까지를 허용할 것인지가 문제가 됨

이를 해결하기 위해 여러 가지 접근방법을 이용할 수 있음

검사비용과 로트를 합격시킨 후 불량이 발생하였을 경우 손실비용 등을 감안하여 가장 경제적인 표본 크기를 정하는 비용적 접근방법도 있을 수 있으며 생산자 및 소비자 위험을 고려하는 확률적 접근방법도 이용할 수 있음

OC 곡선에서 특정한 두 점 ($p_0,\;1-\alpha$)와 $(p_1,\;\beta)$가 있다고 가정할 때

$(p_0,\;1-\alpha)$는 생산자를 만족시키는 점으로 로트의 불량률이 $p_0$일 때 그 로트를 합격시킬 확률이 $P_a = 1 - \alpha$가 되도록 하는 점

여기서 $\alpha$는 불량률 $p_0$에서도 로트가 합격되지 않을 확률이므로 생산자위험에 해당됨

이와 유사하게 $(p_1,\;\beta)$는 소비자를 만족시키는 점으로 불량률이 $p_1$ (소비자에게 바람직하지 않는 수준의 값)일 때 로트의 합격률이 $\beta$에 불과하도록 하는 점 $\rarr \beta$는 소비자 위험에 해당

$\alpha$와 $\beta$값은 비교적 작은 값으로 보통 $\alpha = 0.05, \beta = 0.1$로 정하는 경우가 많음

위와 같은 희망사항을 만족하는 표본 크기 $n$과 합격판정개수 $c$는 따라서 다음 두 개의 방적식에 의해 결정됨

$$\begin{aligned} P_a &= 1-\alpha \quad\quad &p=p_0일\;때 \\ P_a &= \beta \quad\quad &p=p_1일\;때 \end{aligned}$$

실제로는 $n, c$로서 정수값을 원하므로 다음과 같은 부등식을 만족하는 n, c값을 찾는다

$$\begin{aligned} P_a &\geq 1-\alpha \quad\quad &p=p_0일\;때 \\ P_a &\leq \beta \quad\quad &p=p_1일\;때 \end{aligned}$$

$P_a$에는 $n, c$를 포함하고 있음

Uploaded by N2T