An introduction to ROC analysis

T. Fawcett, “An introduction to ROC analysis,” Pattern Recognition Letters, vol. 27, no. 8. Elsevier BV, pp. 861–874, Jun-2006.

ROC (Receiver Operating Characteristic) 은 분류기를 만들고 성능을 시각화하기 좋은 그래프

하지만 이를 실제 사례에 적용할 때 잘못된 이해와 함정에 빠지는 경우가 많음

이 논문은 ROC 그래프에 대한 소개와 연구에 어떻게 적용해야하는지에 대한 가이드를 제공하기 위해 쓰여진 논문

1. Introduction

ROC 그래프는 분류기 (Classifier)의 성능을 시각화하고 이를 바탕으로 선택하기 위해 좋은 도구

특히 hit rate와 false alarm의 trade-off 관계를 보여주기 쉬움

원래 ROC는 의학 진단 시스템에 널리 사용되었지만 Sparckman (1989)에 의해 머신러닝에서도 사용됨

분류 정확도는 성능을 측정하기에 적절한 지표가 아니었기 때문에 새롭게 성능을 측정하기 위해 도입

특히 ROC는 클래스의 분포가 편향되어 있거나 (imbalanced class 문제) 클래스별 분류 비용이 다른 경우에 유용 (금융 FDS 등 오탐했을 때의 비용이 훨씬 큰 경우)

ROC 그래프는 간단한 컨셉을 가지고 있지만 실제 연구에 적용했을 때 복잡함이 생기는 경우가 종종 발생

이는 ROC에 대한 잘못된 이해에서 기인

이 논문은 ROC 그래프에 대한 이해를 돕고 올바르게 사용할 수 있도록 하기 위해 쓰여짐

2. Classifier performance

이진분류를 한다고 할 때 각각의 인스턴스 $I$는 positive와 negative의 라벨을 가지고 있음

분류기들은 이 인스턴스를 분류하기 위해 라벨값만 예측할 수도 있고 p, n에 속할 확률을 예측할 수도 있음 (이 경우 cut-off값이 필요)

예측값과 실제 라벨값 간에는 4가지 가능성이 존재

• True positive - 실제 참이면서 예측값도 참인 경우

• False negative - 실제로는 참이지만 예측값은 거짓인 경우

• True negative - 실제 거짓이면서 예측값도 거짓인 경우

• False positive - 실제 거짓이면서 예측값은 참인 경우

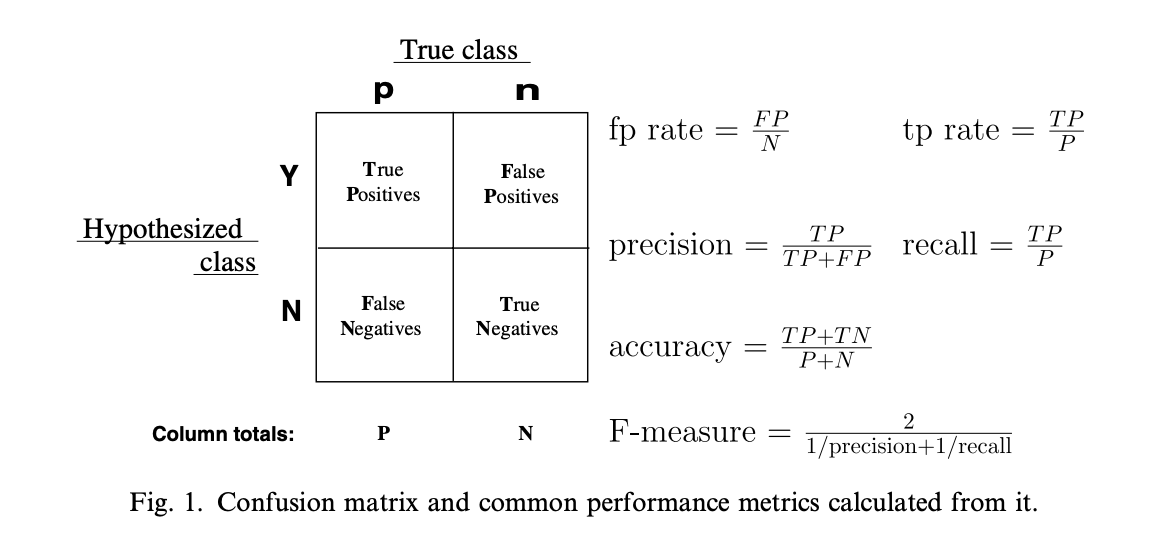
이 4가지 가능성을 표로 표현한 것이 Confusion matrix (contingency table, fig 1)

그 옆의 수식들은 confusion matrix를 통해 계산할 수 있는 지표들

그 외 그림에 없는 수식들

sentivity = recall

specificity = TN / FP + TN (N으로 예측된 것들 중에 실제 N의 비율)

3. ROC space

ROC 그래프는 2차원 그래프로 Y축에는 tp-rate, X축에는 fp-rate

이를 통해 benefit(true positive)와 cost(false positive)의 trade-off를 쉽게 나타낼 수 있음

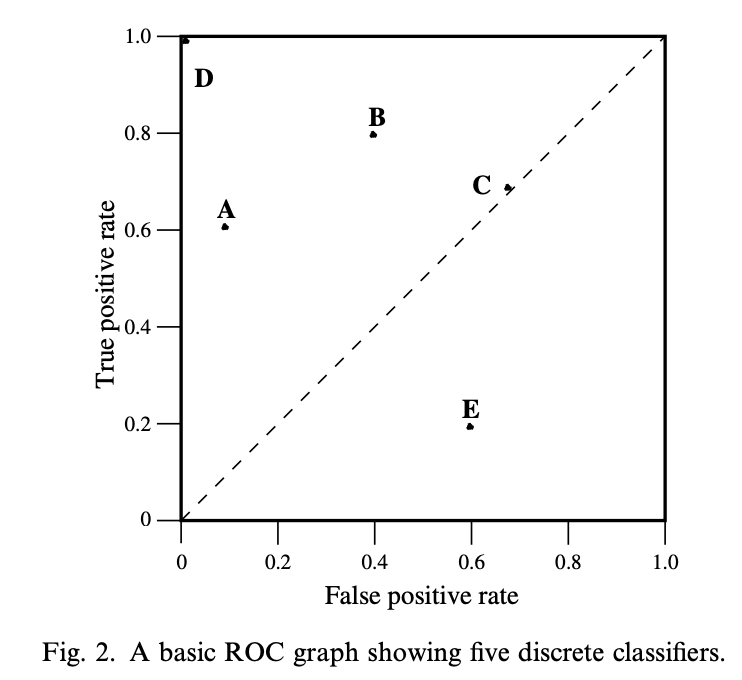
ROC 공간에서 북서쪽으로 갈수록 (tp가 높고 fp가 낮을수록) 성능이 더 좋다고 할 수 있음

3.1 Random performance

y=x인 대각선은 랜덤하게 분류했을 때의 성능을 나타냄

50%의 확률로 p, n을 선택한다고 하면 tp와 fp 모두 0.5가 됨

특정 분류기가 이 대각선 위에 있다는 것은 데이터에 대한 아무런 정보가 없다는 뜻

대각선 아래쪽은 데이터에 대한 정보는 있지만 그것을 잘못 적용하고 있다는 뜻

실제로 fig 2의 B와 E는 정반대임을 알 수 있음

4. Curves in ROC space

특정 분류기들은 결과값으로 Y, N 만을 산출함 (decision tree, rule set 등등)

이런 경우 하나의 confusion matrix만을 만들어 내고 이는 ROC space에서 한 개의 점으로 표현 가능

그에 반해 Naive bayes나 neural network 같은 경우 확률 혹은 점수 를 산출

이 확률은 인스턴스가 특정 클래스일 확률을 의미

이런 확률적 분류기에서 나온 확률들은 정확한 사전적 의미의 확률은 아니지만 확률처럼 사용

이론적으로 threshold를 $-\infin$~$+\infin$으로 변화시켜가면서 ROC ‘커브’를 확인할 수 있지만 너무 비효율적인 방식 (다음 섹션에서 효율적으로 그리는 방법을 설명함)

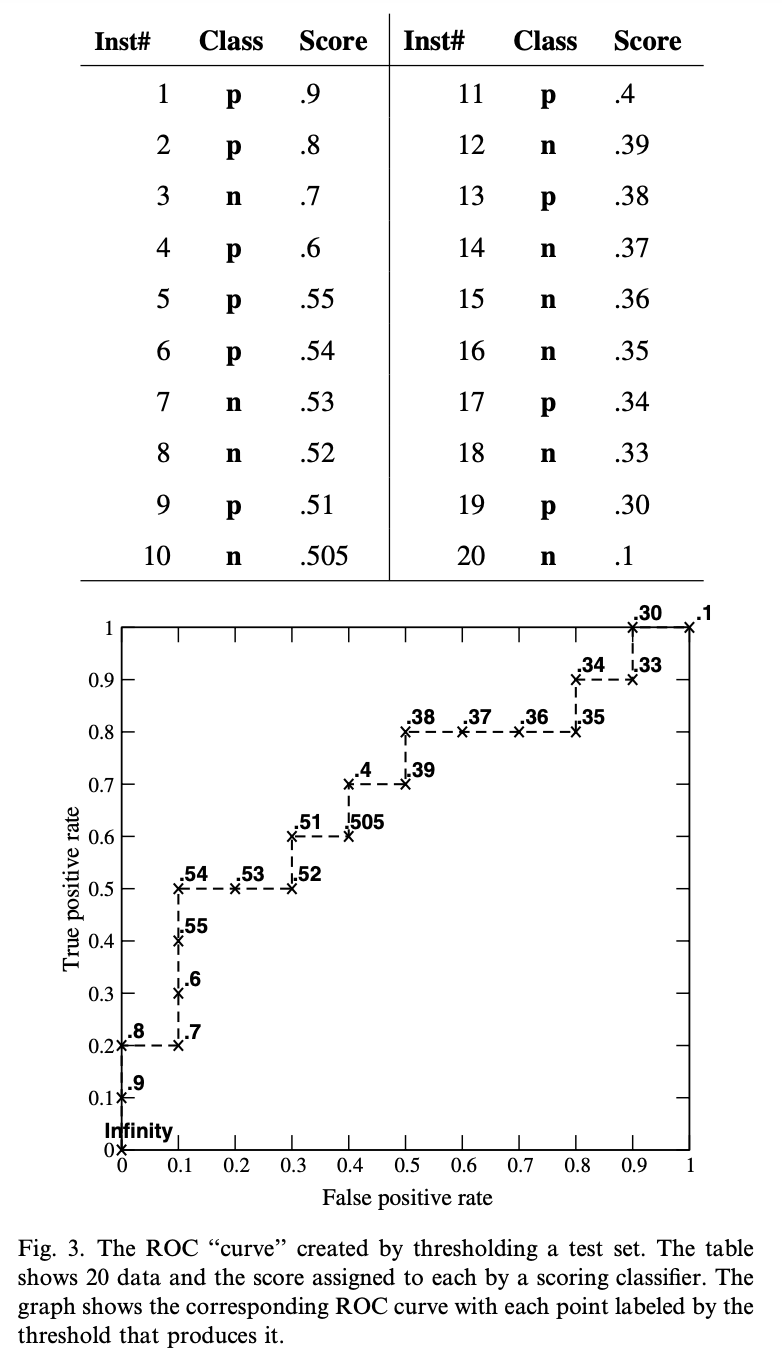
Fig 3은 positive 10개와 negative 10개의 인스턴스를 가지고 ROC 그래프를 그리는 예시

유한한 인스턴스는 fig 3과 같이 계단함수의 형태이고 인스턴스 갯수가 무한대로 갈수록 ‘커브’의 형태에 가까워짐

fig 3에서 우선 인스턴스는 스코어별로 내림차순 정렬되어 있음

ROC 그래프 상의 점들은 score threshold를 나타냄

$+\infin$는 (0,0)을 나타내고 그래프가 오른쪽 위로 가면서 (1,1)로 마무리

fig 3에서 (0.1, 0.5)일 때 accuracy는 70%로 가장 높은 정확도를 나타냄

이 때 threshold는 0.54인데 이는 균형잡힌 클래스 분포일 때 cutoff 0.5보다 0.54가 더 좋음을 의미

4.1 Relative versus absolute scores

ROC 그래프에서 중요한 점은 분류기의 상대적인 인스턴스 score를 생성하는 능력을 평가한다는 점

positive는 확실하게 positive로 negative는 확실하게 negative로 가르는 능력을 측정

모델에서 ‘정확한’ 확률을 생성할 필요없이 상대적인 score만 생성하면 됨

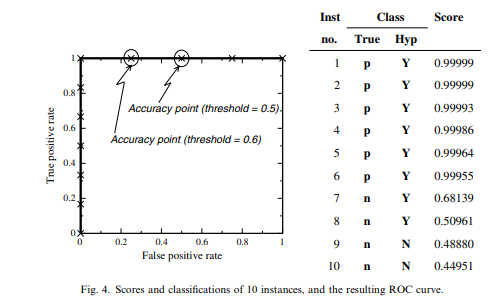
fig 4는 간단한 Naive Bayes 분류기 예시 (컷오프 0.5)

이 분류기의 정확도는 80%이지만 ROC 그래프 상에서는 완벽

이는 positive는 score 순으로 정렬했을 때 negative보다 전부 위에 있기 때문

분류기에서 나온 ‘확률’은 정확한 의미의 확률이 아니기 때문에 컷오프 0.5로 분류하는 것은 부적절하므로 위와 같은 결과가 나옴

사전에 클래스 분포를 알고 있어서 이를 사전확률로 사용한다면 $P(p) = 0.6$ 이므로 컷오프는 0.6이 되고 이 때의 정확도도 90% (그러나 최적의 성능은 내지 못함)

분류기의 score는 상대적이므로 클래스간 직접적인 비교는 부적절함

어떤 모델의 ‘확률’은 [0,1]이고 다른 모델 [-1, 1] 일수도 있기 때문 (실제 라이브러리는 이렇지는 않지만) 에 컷오프값을 이용해서 모델 성능을 비교하는 것은 의미가 없음

4.2 Class skew

ROC 그래프는 클래스의 분포에 둔감한 특성을 가지고 있음

positive, negative 비율이 바뀌어도 ROC 그래프는 변하지 않음

fig 1의 confusion matrix 에서 다른 지표들은 모두 두 열에서 값을 사용

이는 한 비율이 바뀌면 값이 바뀌게 됨 (precision만 해도 TP/(FP+TP) 이므로 바뀜)

ROC는 각각의 열에서만 계산하는 tp rate와 fp rate만 사용하므로 클래스 분포에 영향을 받지 않음

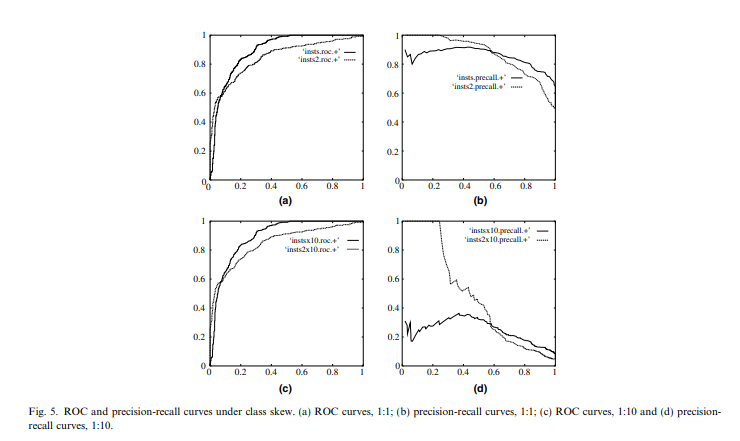
fig 5는 클래스 분포가 변할 때 ROC 그래프와 precision-recall 그래프

클래스 분포가 변해도 ROC (a, c)는 변하지 않지만 precision-recall (b, d)는 크게 변함

4.3 Creating scoring classifiers

4.3 절의 내용은 score를 생성하는 분류기를 만드는 방법에 대한 내용

분류기는 원래 Y, N의 이산적인 값만 산출하는데 이럴 경우 ROC 그래프는 계단함수 형태

정확한 ‘곡선’을 만들기 위해서는 score 형태로 변환 필요

그래서 어떻게 분류기에서 이런 score를 만들어 낼 수 있는가에 대한 내용

예를 들어 Decision tree 류들은 클래스가 leaf node에서 클래스 비율에 따라 결정되는데 이를 그대로 score로 사용할 수 있음

scikit-learn의 분류기들은 predict_proba() 함수를 통해 score값을 알 수 있으므로 편리

5. Efficient generation of ROC curves

알고리즘 1은 ROC 커브를 효율적으로 만드는 방법을 설명

특정 인스턴스가 어떤 threshold에서 positive로 분류되었다면 그보다 작은 threshold에서는 모두 positive로 분류된다는 사실을 활용

score 값에 따라 인스턴스를 정렬한 후 이 방식을 적용하면 선형 탐색 (linear scan)만으로 ROC 그래프를 그릴 수 있음

내림차순으로 정렬하는데 $O(n \log n)$, 선형탐색 후 ROC 그래프를 만드는데 $O(n)$이 소요되어 총 $O(n \log n)$이 소요

알고리즘에서 중요한 점은 score가 이전 score와 다를 때만 ROC를 계산한다는 점

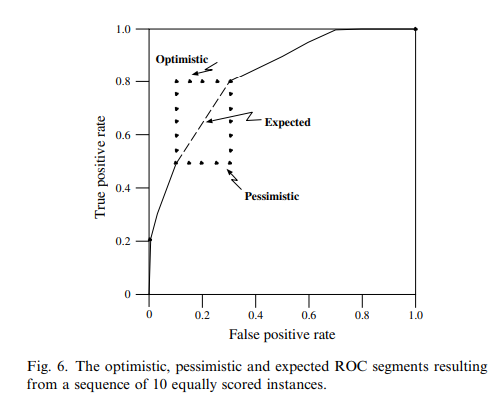
fig 6은 score가 같은 인스턴스 10개 (positive 6, negative 4)에 대한 ‘optimistic’한 그래프와 ‘pessimistic’한 극단적인 그래프를 나타냄

‘낙관적인’ 경우는 positive 6개를 먼저 처리한 후 negative를 처리하는 경우, ‘비관적인’ 경우는 그 반대 상황 (순서가 섞여있다면 계단함수 모양으로 나타남)

ROC 그래프는 분류기의 예상 성능을 나타내므로 다른 정보가 없다면 ‘낙관적인’ 경우와 ‘비관적인’ 경우의 평균을 보여줘야함

여기서 평균은 사각형의 대각선이므로 score가 다른 인스턴스가 들어오기 전까진 업데이트 불필요

이걸 처리하기 위한 방법이 7번째 줄 $f_{prev}$의 역할

6. The ROC convex hull

ROC 그래프의 또 다른 장점은 클래스 분포나 error cost에 관계없이 분류기 성능을 시각화할 수 있어편향된 분포를 가지고 있거나 error cost가 중요한 경우에 유용

여러 분류기들을 평가하고자 할 때 ROC 그래프로 비교하게 되면 클래스 분포(class-skew)나 오류비용이 변하더라도 ROC 그래프 자체는 변하지 않음

결국 이런 조건이 변하면 선택하고자 하는 분류기는 조건에 맞게 바뀔 수 있어도 그래프 자체는 변하지 않음

Provost and Fawcett (1988, 2001)은 운영 조건들을 iso-performance line 으로 쉽게 변환할 수 있는 수식을 제시

ROC 공간에서 두 점 $(TP_1, FP_1), (TP_2, FP_2)$는 아래 수식을 만족하면 같은 성능을 가짐

$$\frac{TP_2 - TP_1}{FP_2 - FP_1} = \frac{c(Y, n)p(n)}{c(N, p)p(p)} = m$$

$c(Y, n)$은 false positive 비용, $c(N, p)$는 false negative 비용

위 식에서 m은 iso-performance line의 기울기를 결정하고 각각의 운영 조건들이 이런 iso-performance line을 만들어내고 line들이 좀 더 ‘북서쪽’에 가까울수록 (TP-절편이 클수록) 비용이 작고 더 좋은 성능을 가진다고 할 수 있음 (fig7a)

일반적으로 convex hull에 접할때만 최적이라고 할 수 있는데 ROC 공간 내에서 convex hull을 ROCCH 라고 함

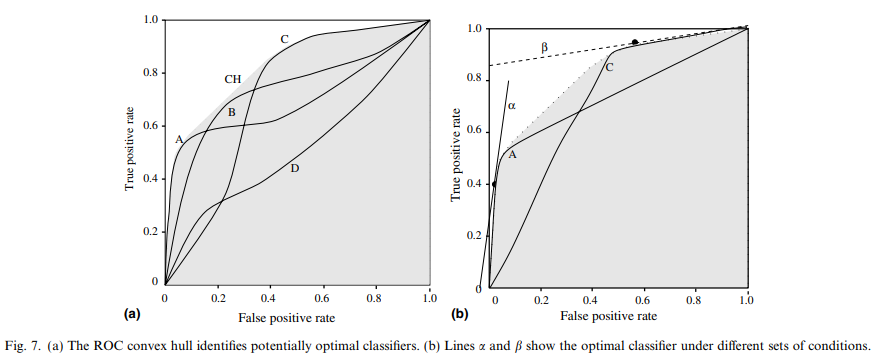
fig7a는 4개의 분류기에 대한 ROC 커브와 CH를 나타낸 그림

여기서 B, D는 CH에 접하고 있지 않으므로 최적이 아님(sub-optimal)

가장 높은 분류성능을 내는 분류기를 찾는다면 CH에 접하고 있는 A, C 중에서 골라야함

만약 negative가 positive보다 10배 많고 오분류의 비용이 같으면 $m=10$ 이고 이 때 최적곡선은 fig 8b의 $\alpha$ 이므로 A 가 이 조건에서 가장 성능이 좋은 분류기가 됨

negative와 positive의 수는 같고 false negative 비용이 10배 더 높다면 $m=\frac{1}{10}$이고 이 때의 최적곡선은 $\beta$ 이므로 B가 가장 최적 분류기가 됨

7. Area under an ROC curve (AUC)

ROC 커브는 2차원 값이기 때문에 분류기 성능을 한눈에 비교하기 어렵기 때문에 비교하기 쉽도록 단일 스칼라 값으로 만든 것이 바로 AUC

AUC는 0, 1 사이의 값을 가지지만 랜덤으로 분류해도 0.5 이상은 나오므로 AUC가 0.5보다 작은 분류기는 존재할 수 없음 (ROC 공간에서 대각선)

AUC에는 무작위로 선택한 positive를 무작위로 선택한 negative보다 높은 rank를 줄 확률이라는 중요한 통계적 성질이 존재함

또한 $Gini + 1 = 2 \times AUC$ 로 Gini coefficient와도 밀접한 관련이 있음

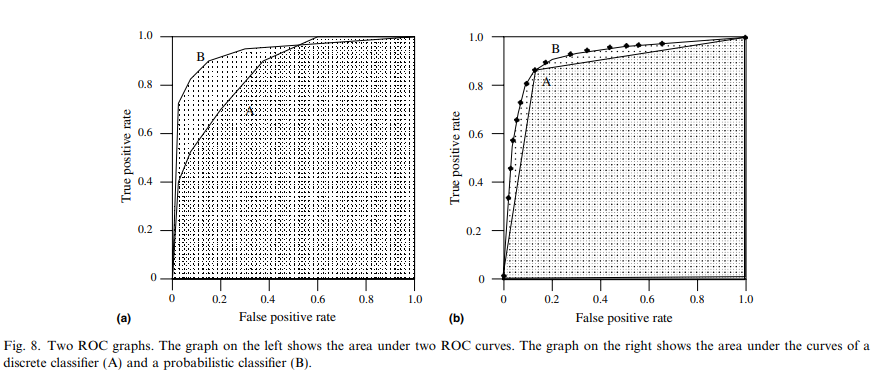
fig 8a는 두 개의 분류기 A, B에 대한 ROC 커브

AUC가 B가 더 크므로 B가 더 좋은 성능을 가진다고 할 수 있음

fig 8b는 이진 분류기 A와 score 분류기 B를 비교한 그래프

A는 고정된 threshold를 사용한 B의 성능을 나타내는데 특정 지점까지는 (A의 threshold) 두 분류기의 성능이 동일하지만 그 지점을 넘어서면 B의 성능이 더 좋아짐

fig 8a 에서 B는 A보다 높은 AUC를 가지고 있지만 fp rate 0.6에서는 A가 더 좋은 모습을 보임

이런 경우가 있을수도 있지만 일반적으로 높은 AUC는 더 좋은 성능을 보장함

AUC는 알고리즘1을 조금 수정해서 쉽게 계산이 가능 (아래 알고리즘2)

8. Averaging ROC curves

ROC 커브가 분류기 성능을 평가하는 척도이지만 단순히 그래프를 그리고 더 좋은 분류기를 선택하는 것은 잘못된 방법

각 분류기들의 분산 정보가 없다면 ‘더 나은’ 분류기를 선택할 수 없음

원본 인스턴스가 존재한다면 하나의 큰 데이터셋으로 합친 후 ROC를 구할 수 있지만 이렇게 합치게 되면 원래 목적인 분산을 구하는 것은 할 수 없음

ROC 커브는 2차원이기 때문에 1차원인 평균을 구하기 위해서는 투영이 필요

ROC 커브를 투사하는 방법은 vertical, threshold 두 가지 방법이 존재

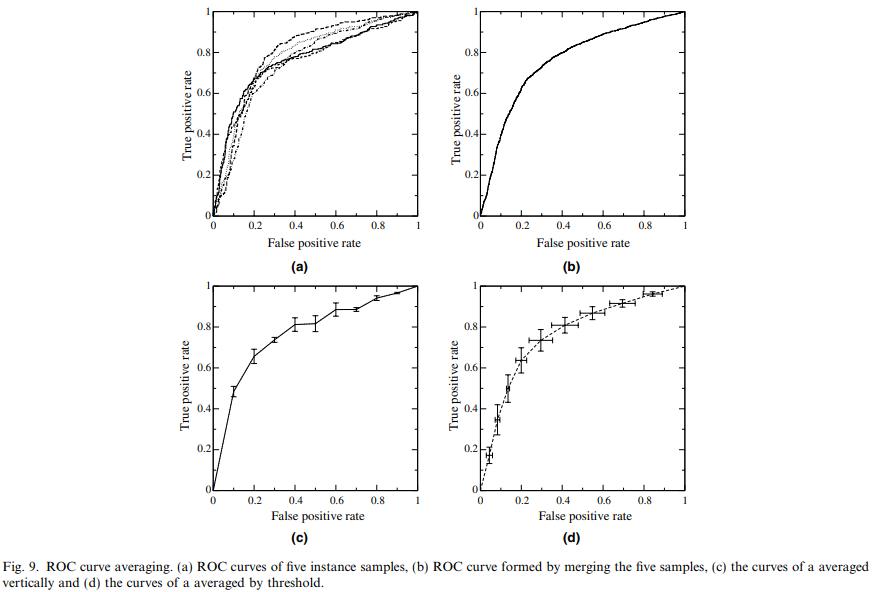
아래 그림의 a는 평균을 내야할 5개의 ROC 커브 (각각 1000개의 인스턴스)

b는 인스턴스를 하나로 합친 후 그린 ROC 커브

c, d 는 vertical, threshold averaging 후의 ROC 커브

8.1 Vertical averaging

vertical averaging은 고정된 fp rate에 대해 tp rate들을 평균하는 방법

이 방법은 실제로 fp rate를 고정할 수 있거나 단일 차원의 변동을 측정하고자 할 때 사용

ROC 커브를 하나의 함수로 보고 $tp \; rate = R_i(fp\;rate)$ 로 fp rate별로 가장 큰 tp rate 선택하고 필요한 부분은 보간(interpolate) 하여 사용

ROC 커브의 평균 $\hat{R}(fp\;rate)= mean[R_i(fp\;rate)]$

평균 ROC 커브는 각 fp rate에 맞는 $\hat{R}$를 이용해서 그릴 수 있고 각 tp rate의 신뢰구간은 이항분포를 가정하여 계산함

fig 9c 는 fp rate 0.1마다 vertical averaging을 적용한 그래프

아래 알고리즘 3을 사용하여 vertical averaging을 구할 수 있음

8.2 Threshold averaging

vertical averaging은 fp rate를 고정하고 계산하는 방식이지만 실제로 fp rate를 고정하기 어려움

threshold averaging은 통제할 수 있는 threshold값들에 대해 평균을 계산하는 방식

아래 알고리즘 4는 threshold averaging을 하는 방법을 나타냄

각 threshold 별로 해당 값보다 작거나 같은 가장 큰 점들을 선택하게 되는데 (vertical의 함수와 유사) tp, fp 별로 이루어짐 (X, Y축 모두, fig 9d에서 십자가 형태의 신뢰구간이 나타나는 이유)

threshold 평균을 사용하기 위해서는 분류기가 반드시 score를 산출해줘야함

또한 4.1에서 설명한 것과 같이 서로 다른 모델에서는 score 직접 비교가 오해가 있을 수 있으므로 유의해서 사용해야함

9. Decision problems with more than two classes

지금까지 살펴본 ROC 문제는 전부 두 개의 클래스 분류 문제

클래스가 두 개밖에 없으면 2차원에 표현이 가능하고 대칭적이기 때문에 쉽게 해석이 가능

9.1 Multi-class ROC graphs

n개의 클래스가 있는 경우 훨씬 복잡한 공간을 다뤄야함

$n^2$ confusion matrix에서 주 대각선 $n$ 만큼의 정확한 분류와 $n^2 - n$ 만큼의 오분류가 존재

n 클래스를 다루는 쉬운 방법은 class-reference 방식

전체 클래스가 $C$개이고 현재 클래스가 $c_i$이면 $c_i$를 제외한 다른 클래스는 음성으로 간주

$$P_i = c_i \\ N_i = \bigcup_{j \neq i} c_j \in C$$

이 방법은 다중 클래스를 다루는 편리한 방법이지만 클래스 분포에 둔감한 ROC의 장점을 저해함

$N_i$는 $c_i$가 아닌 모든 클래스의 합이므로 클래스 분포가 변하면 ROC가 변하게 됨

9.2 Multi-class AUC

다중 클래스에서는 AUC 계산도 어려움 (AUC의 의미부터 2차원에서 계산되는 값)

Provost and Domingos (2001) 에서 제시한 방법은 probability estimation tree를 이용한 방법

class-reference 방법으로 ROC를 생성한 후 각 클래스에 대해 AUC를 계산한 다음 모두 더하는 방식

$$AUC_{total} = \sum_{c_j \in C} AUC(c_j) \cdot p(c_j)$$

이 방식은 계산하기 쉽고 시각화하기 쉬운 장점이 있지만 class-reference와 마찬가지로 클래스 분포에 민감하다는 단점을 가지고 있음

Hand and Till (2001) 은 다른 방식으로 multi-class AUC를 계산

이 방식은 AUC가 분류기가 임의의 positive를 임의의 negative 보다 높은 순위를 매길 확률과 동일하다는 사실에 기반하여 클래스 분포와 오류 비용에 덜 민감하도록 설계됨

여기서 $M$이라는 클래스 간 가중치가 없는 측정치를 사용

$$AUC_{total} = \frac{2}{|C|(|C|-1)}\sum_{(c_i, c_j) \in C}AUC(c_i,c_j)$$

이 방식은 확률적으로 올바른 방식이지만 시각화하기는 어려움

10. Interpolating classifiers

원하는 성능의 분류기가 없을 경우 여러 개의 분류기를 함께 사용할 수도 있음

이 장은 여러 개의 분류기에서 샘플링하여 원하는 성능을 맞추는 방법을 설명함

CoIL Challenge 2000 (van der Putten and Someren, 2000) 예제

4000명의 고객에게 새로운 보험 상품을 권유하는데 예산 문제로 800명에게만 발송하고자 함

가장 확률이 높은 800명을 선택하기 위해 예측을 진행하는데 예상 응답률은 6%이므로 240명의 응답(positive)와 3760명의 비응답자(negative)가 예상됨 (각각 4000 * 0.06, 4000 * 0.94)

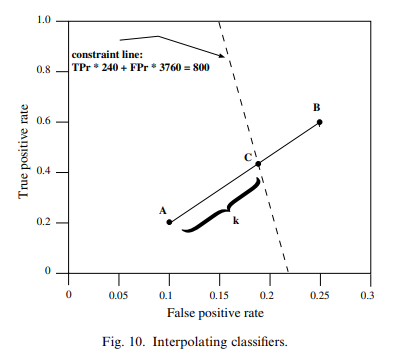
분류기 A, B는 각각 (0.1, 0.2), (0.25, 0.6)의 fp, tp rate를 가짐

여기서 원하는 사람의 숫자는 800명이므로 $fp\;rate \times 3760 + tp\;rate \times 240 = 800$

A를 사용하면 $0.1 \times 3760 + 0.2 \times 240 = 424$ 이므로 너무 작음

B를 사용하면 $0.25 \times 3760 + 0.6 \times 240=1084$ 이므로 너무 많음

fig 10의 점선은 정확하게 원하는 숫자를 만들어낼 수 있는 선

여기서 점 C 는 대략 (0.18, 0.42)에 해당하는데 이는 A,B 선형보간을 통해 만들어낼 수 있음

C가 AB 선분사이에서 위치한 거리를 $k$ 라고 하면 $k$는 아래와 같은 식으로 계산 가능

$$k = \frac{0.18 - 0.1}{0.25 -0.1} \approx 0.53$$

따라서 B를 0.53만큼 샘플링하고 A를 1-0.53=0.47 만큼 샘플링하면 원하는 결과를 얻을 수 있음

실제로 이를 적용하는 방법은 0, 1 사이를 무작위로 샘플링한 후 값이 0.53보다 크면 B의 값을 취하는 것으로 적용할 수 있음

11. Conclusion

💡

ROC 커브는 분류기 성능을 시각화하고 평가하는데 매우 유용한 도구

💡

accuracy, precision, recall 등과 같은 스칼라 값 지표보다 다양한 측면의 지표를 제공함으로써 분류기를 좀 더 세밀하게 평가할 수 있음

💡

또한 클래스 분포나 오분류 비용에 무관하게 그릴 수 있어서 다른 지표들에 비해 유용

💡

하지만 ROC 역시 명확한 이해를 바탕으로 사용해야 함

Uploaded by N2T