11장. 실험계획법

실험계획법(design of experiments) - 실험에 대한 설계 및 분석방법 품질 및 공정최적화를 위해서 어떻게 실험을 행하고, 데이터를 어떻게 취하며, 어떠한 통계적 방법으로 데이터를 분석할 것인가를 계획하는 것

11.1 실험계획의 기본개념

11.1.1 인자 및 수준

인자(factor) - 제품 등의 품질이나 공정에 영향을 주는 주요 요인으로 판단되어 실험에서 관심의 대상이 되는 변수

해당 인자에 대해 몇 가지로 나뉘는 실험조건, 즉 인자를 양적 또는 질적으로 변화시킬 경우의 단계를 그 인자의 수준(level)이라고 함

이 때 인자들의 각 수준들의 조합을 수준조합 또는 처리조건(treatment)라 부름

11.1.2 교호작용

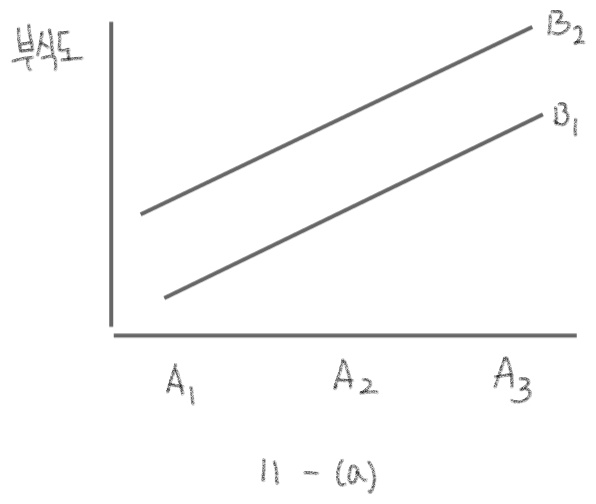
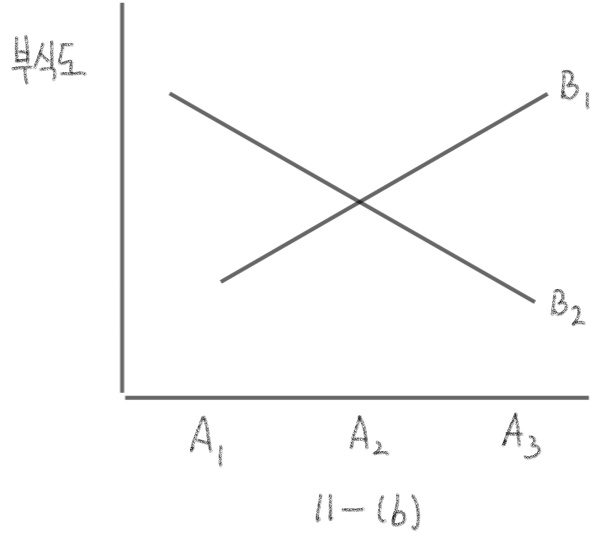
어떤 품질요인으로 다수의 인자가 관여될 수 있으며 또한 두 개 이상의 인자를 취급할 때는 두 인자 간의 교호작용(interaction)이 있을 수 있음 한 인자의 수준에 따른 종속변수의 변화가 다른 인자의 수준에 따라 다르게 나타날 때, 두 인자 간의 교호작용이 있다고 함

예를 들어 알루미늄 부식에 코팅방식(A인자)와 습도(B인자)의 두 인자가 영향을 준다고 가정할 때 코팅방식의 세 수준(각각 $A_1, A_2, A_3$)과 습도의 두 수준(각각 $B_1, B_2$)에서 실험을 하고 알루미늄 부식도를 측정하여 11-(a)와 같은 결과를 보인다면 코팅방식과 습도수준이 각각 부식도에 영향을 주지만 두 인자의 결합에 의한 더 이상의 영향은 없다는 것을 의미

($A_3, B_2$)에서의 부식도를 ($A_1, B_1$)조합에서 부식도와 비교할 때 인자 A의 수준 변화에 의한 증가량에 인자 B의 수준 변화에 따른 증가량을 합한 형태로 나타남

두 인자 간의 교호작용이 있는 경우 11-(b)와 같은 형태를 보임

11.1.3 실험계획법의 종류

주요 실험계획법으로는 다음과 같은 방법들이 있다.

1. 일원배치법(single factor design) 한 인자의 영향을 조사하기 위한 실험계획법 일원배치법은 각 실험처리에 대해 실험단위를 완전히 랜덤하게 배치하여 실험하는 방법이므로 완전무작위계획법(completely randomized design)이라고도 함

2. 이원배치법(two-factor design) 두 개의 인자에 대해 그 영향을 조사할 때 쓰이는 방법 각 인자의 수준 수는 다를 수 있으며 모든 수준조합에 대해 실험을 진행 이 때 각 수준조합에 대해 반복적으로 실험을 행할 수도 있음 이원배치법을 확장하여 두 개 이상의 인자를 포함한 실험을 다원배치법이라 함

3. 요인배치법(factorial design)

   각 인자의 수준수를 동일하게 설계하여 실험을 행하는 방법 인자수가 n개 있고 각 인자의 수준이 2라면 $2^n$형 요인배치법, 3 수준의 경우는 $3^n$형 요인배치법이라 함

4. 일부실시법(fractional factorial design) 각 인자의 수준조합 중에서 일부만 선택하여 실험횟수를 가능한 적게 하는 방법 대신 불필요한 교호작용은 분석하지 않음

11.1.4 실험계획법의 순서

실험연구는 실험목적의 정의, 실험계획, 실험의 진행, 자료의 분석, 결과의 해석의 과정을 거침 세부적인 단계를 아래와 같다

1단계: 실험목적을 설정하고 구체적인 문제를 정의하며 연구가설을 세움

2단계: 실험목적에 따른 반응치 설정. 이 때 측정가능성 및 반응치에 대한 타인자의 영향은 없는지 고려

3단계: 인자와 인자의 수준을 결정. 인자의 수준을 나눌 때는 실험에 드는 시간 및 비용도 고려해야함

4단계: 실험의 배치방법과 실험순서를 정함. 실험장비의 배치는 실험이 용이하고 외부환경의 영향을 통제할 수 있도록 해야함. 실험순서에 민감한 실험인 경우에는 무작위로 실험순서를 정해야 함

5단계: 실험 실시. 예비 실험을 통해 실험방법을 보완할 수도 있음

6단계: 데이터를 분석하고 결과 해석. 인자의 유의성을 판정하기 위해서는 주로 분산분석법을 사용하며, 필요시 수준조합별 평균의 점추정 또는 신뢰구간을 산출. 결측치는 분석 전에 미리 적절한 조치를 취해주어야함 품질 또는 공정 최적화를 목적으로 행한 실험의 경우 영향인자를 추출하고 최적 수준조합을 도출

11.2 일원배치법

인자가 하나인 실험에 대한 설계를 일원배치법이라 함

인자의 수준수가 $a$이고 각 수준에서 실험반복수가 $r$일 때 총 $ar$번의 실험이 요구되며 완전무작위계획법에 의해 실험 실시

인자 A의 수준이 a개 이고, 각 수준에서 반복수가 r일 때 일원배치법에 의한 i번째 수준에서 j번째 반복으로부터 얻어진 실험결과치를 $Y_{ij}$라 하면, 이를 설명하는 모형은 다음과 같다

$$\tag{11.1} \begin{align*} Y_{ij} &= \mu_i + \varepsilon_{ij}, \,\,i = 1, 2, \,\,, j = 1, 2, \dots, r \\ \mu_i &= \mu + \alpha_i \end{align*}$$

여기서 $\mu_i$는 인자 A의 i번째 수준에서의 평균을 의미

이는 다시 전체평균 $\mu$와 인자 A의 i번째 수준이 주는 효과 $\alpha_i$의 합으로 표시된다고 가정

수준에 따라 평균이 다르다는 것은 $\alpha_i$가 수준 i에 따라 서로 다름을 의미

어떤 수준 i에서 평균이 전체 평균($\mu$)보다 크다면 $\alpha_i > 0$을 나타냄

어떤 수준 j에서 평균이 전체 평균보다 작으면 $\alpha_j < 0$이 됨

따라서 $\sum \alpha_i = 0$ 이 됨

오차항 $\varepsilon_i$는 서로 독립이며 수준과 관계없이 평균 0, 분산 $\sigma^2$인 정규분포를 따른다고 가정

i번째 수준의 (표본)평균 $\bar Y_i$, 전체 관측값의 총평균 $\bar Y$는 다음과 같음

$$\begin{align*} \bar Y_i &= \frac{1}{r}\sum_{j=1}^{r}Y_{ij} = \frac{T_i}{r}, \,\, i = 1, 2, \dots, \alpha \\ \bar Y &= \frac{1}{ar}\sum_{i=1}^{\alpha}\sum_{j=1}^{r}Y_{ij} = \frac{T}{ar} \end{align*}$$

<표 11-1> 일원배치법의 데이터구조

	인자의 수준
실험의 반복	$\begin{matrix}A_1&&A_2&&\dots&&A_n\\Y_{11}&&Y_{21}&&\dots&&Y_{a1}\\Y_{12}&&Y_{22}&&\dots&&Y_{a2}\\\vdots&&\vdots&&&&\vdots\\Y_{1r}&&Y_{2r}&&\dots&&Y_{ar}\end{matrix}$
합/평균	$\begin{matrix}T_1&&T_2&&\dots&&T_a\\\bar Y_1&&\bar Y_2 &&\dots&&\bar Y_a\end{matrix}$	$\begin{matrix}T\\\bar Y\end{matrix}$

관심사는 인자 A의 수준을 변화시킬 때 평균반응치가 변하는 지 여부

인자수준이 변할 때 반응치가 심하게 변할수록 그 인자가 큰 영향을 준다고 할 수 있음

인자수준이 변해도 반응치가 변하지 않으면 그 인자는 영향요인이 아니라고 할 수 있음

수준별 평균($\mu_i$)이 서로 동일한가 여부는 수준별 효과인 $\alpha_i$들이 서로 동일한가 여부를 다루는 것과 같음

따라서 다음과 같은 가설을 검정하고자 함

$$\tag{11.2} \begin{aligned} H_0 &: \alpha_1 = \alpha_2 = \dots = \alpha_{\alpha} = 0 \\ H_1 &: \alpha_i \neq 0 \end{aligned}$$

귀무가설 $H_0$이 기각될 때 인자 A의 수준별 평균이 서로 동일하지 않다고 말하며 인자 A가 유의하다고 함

식 11.2 의 가설을 검정하기 위해 다중회귀분석에서 F검정하는 방법과 유사한 방법 사용

즉 오차항의 분산 $\sigma^2$의 두 가지 추정량 사용

$H_0$의 진위와 관계없이 사용할 수 있는 $\sigma^2$의 추정량을 유도하고 $H_0$가 옳을 때만 사용할 수 있는 $\sigma^2$의 추정량을 유도하여 그 비를 검정통계량으로 이용

이를 위해서 우선 회귀분석에서와 마찬가지로 전체제곱합을 분해하여야 함

전체제곱합(SST)는 다음과 같이 오차제곱합(잔차제곱합)과 인자 A에 의한 제곱합으로 나눌 수 있다

$$\tag{11.3} \sum_i\sum_j(Y_{ij} - \bar Y \dots )^2 = r\sum_i(\bar Y_i - \bar Y \dots)^2 + \sum_i\sum_j(Y_{ij} - \bar Y_{i}\dots)^2$$

총제곱합(SST) = 인자 A의 제곱합(SSA) + 오차제곱합(SSE)

SSA는 인자 A의 각 수준에서의 평균과 전체 평균과의 차의 제곱합으로 자유도 (a-1)

SSE는 서로 독립인 a개의 수준에서 각 관측값과 수준평균과의 차의 제곱합

한 수준내의 자유도가 각각 r-1이 되어 SSE의 자유도는 a(r-1)

따라서 평균제곱은 다음과 같이 각각의 제곱합을 자유도로 나눈 값이다

인자 A 평균제곱 MSA = SSA /(a-1)

오차평균제곱 MSE = SSE/a(r-1)

여기서 MSE는 가설과 관계없이 항상 $\sigma^2$의 불편추정량이 되며 MSA는 가설 $H_0$가 옳을 때 $\sigma^2$의 불편추정량으로 사용가능

식 11.3에서 SSA를 구하기 위해 $\bar Y_i$와 $\bar Y$의 차를 고려하는데 $H_0$가 옳지 않다는 것은 수준별 평균과 전체 평균이 다르다는 것이므로, 이 경우 $(\bar Y_i - \bar Y)$는 오차에 의한 것만이 아니기 때문에 이 차를 바탕으로 오차 분산을 추정할 수는 없음

따라서 식 11.2의 가설에 대한 검정통계량은 다음과 같다

$$\tag{11.4} F = \frac{MSA}{MSE}$$

식 11.4에 의해 구한 F값이 1보다 매우 크다는 것은 MSA가 MSE와는 상당히 다른 값을 갖는 것을 의미하므로 MSA를 $\sigma^2$의 불편추정량으로 사용할 수 없고 따라서 가설 $H_0$를 기각하게 됨

검정통계량 F는 가설 $H_0$가 옳을 때 자유도가 (a-1, a(r-1))인 F분포를 따르는 사실을 이용하여 다음과 같을 때 유의수준에서 가설 $H_0$를 기각하며 인자 A가 유의한 영향을 준다고 판단

$$F > F_{(\alpha;\, a-1,a(r-1))}$$

여기서도 F값이 1보다 큰 경우만 관심에 두기 때문에 단측검정에 해당

회귀분석에서와 같이 F값에 대응한 p값이 산출되면 보다 용이하게 다앙한 유의수준에서 검정 실시 가능

이와 같은 과정을 정리하면 아래 표 11-2와 같은 분산분석표로 요약할 수 있음

<표 11-2> 일원배치법의 분산분석표

변동요인	자유도	제곱합	평균제곱	$F-$값
인자 A	$a-1$	$SSA$	$MSA$	$F=MSA/MSE$
오차	$a(r-1)$	$SSE$	$MSE$
전체	$ar-1$	$SST$

11.3 이원배치법

두 개의 인자를 취해 실험을 하는 방법 두 개의 인자 A와 B의 수준들의 조합에 대한 실험을 하여 각 인자의 영향을 조사하는 것

11.3.1 반복이 없는 이원배치법

인자 A의 수준이 a개 이고 인자 B의 수준이 b개일 때 모든 실험처리조합에 대해서 한번씩의 실험을 행하는 경우 반복이 없는 이원배치법의 데이터 구조식은 다음과 같음

$$\tag{11.5} Y_{ij} = \mu_{ij} + \varepsilon_{ij}, \,\,i= 1,2,\dots, a; \,\, j = 1,2,\dots,b;$$

$$\mu_{ij} = \mu + a_i + b_j$$

$\mu_{ij}$ = 인자 A의 i수준과 인자 B의 j수준 조합에서의 평균 반응치

$\mu$ = 전체 평균

$a_i$ = 인자 A의 i 수준에 의한 효과

$b_j$ = 인자 B의 j 수준에 의한 효과

<표 11-3> 반복이 없는 이원배치법의 데이터 구조

인자 B \ 인자 A	$\begin{matrix}A_1&&A_2&&\dots&&A_a\end{matrix}$	합	평균
$\begin{matrix}B_1\\B_2\\\vdots\\B_b\end{matrix}$	$\begin{matrix}Y_{11}&&Y_{21}&&\dots&&Y_{a1}\\Y_{12}&&Y_{22}&&\dots&&Y_{a2}\\\vdots&&\vdots&&&&\vdots\\Y_{1b}&&Y_{2b}&&\dots&&Y_{ab}\\\end{matrix}$	$\begin{matrix}T_1\\T_2\\\vdots\\T_b\end{matrix}$	$\begin{matrix}\bar Y_1\\\bar Y_2\\\vdots\\\bar Y_b\end{matrix}$
합	$\begin{matrix}T_1&&T_2&&\dots&&T_a\end{matrix}$	$T$
평균	$\begin{matrix}\bar Y_1&&\bar Y_2&&\dots&&\bar Y_a\end{matrix}$		$\bar Y$

여기서 관심사는 인자 A의 수준 변화에 따라 반응치에 차이가 있는지, 인자 B의 수준변화에 따라 반응치에 차이가 있는지 여부

이를 다음과 같은 귀무가설로 표현할 수 있음

$$\tag{11.6a} H_{0A} : \alpha_1 = \alpha_2 = \dots = \alpha_a = 0$$

$$\tag{11.6b} H_{0B} = \beta_1 = \beta_2 = \dots = \beta_b = 0$$

이 가설을 검정하기 위해 분산분석표 작성 필요

전체제곱합은 다음과 같이 분해할 수 있음

$$\begin{aligned} SST &= \sum_{i=1}^a \sum_{j=1}^b (Y_{ij} - \bar Y ..)^2 \\ &= \sum_i \sum_j (\bar Y_{i.} - \bar Y..)^2 + \sum_i \sum_j (\bar Y_{.j} - \bar Y ..)^2 + \sum_i \sum_j (Y_{ij}-\bar Y_{i.} - \bar Y_{.j}+\bar Y..)^2 \\ &= SSA + SSB + SSE \end{aligned}$$

여기서 SSA는 인자 A의 제곱합 - 관련 자유도는 (a-1)

SSB는 인자 B의 제곱합이며 관련 자유도 (b-1)

일원배치법과 유사한 방법으로 평균제곱을 산출하고 분산분석표를 작성하면 다음 표와 같음

<표 11-4> 반복이 없는 이원배치법의 분산분석표

변동요인	제곱합	자유도	평균제곱	F-값
인자 A	SSA	a-1	MSA=SSA/(a-1)	$F_A$=MSA/MSE
인자 B	SSB	b-1	MSB=SSB/(b-1)	$F_B$=MSB/MSE
오차	SSE	(a-1)(b-1)	MSE=SSE/(a-1)(b-1)
전체	SST	ab-1

MSE는 가설과 관계없이 $\sigma^2$의 불편추정량이 됨

MSA는 식 11.6a의 가설 $H_{0A}$가 옳을 때 $\sigma^2$의 불편추정량이 됨 MSB는 식 11.6b의 가설 $H_{0B}$가 옳을 때 $\sigma^2$의 불편추정량이 됨

따라서 다음 두 개의 F-값을 산출하여 유의수준에 대해 가설을 검정함

$$\begin{aligned} F_A &> F_{(\alpha; a-1, (a-1)(b-1))}\, 이면, \,H_{0A}\,기각 \\ F_B &> F_{(\alpha; b-1, (a-1)(b-1))}\, 이면, \,H_{0B}\,기각 \\ \end{aligned}$$

11.3.2 반복이 있는 이원배치법

반복이 없는 이원배치법에서는 두 인자의 수준들의 조합에 대해 한번의 실험을 함 가능하다면 2번 이상의 실험을 하는 것이 바람직

본 절에서는 수준조합당 실험 반복을 r번씩 하는 경우를 다룸 반복이 있는 이원배치법에서는 두 인자의 교호작용(interaction)에 대한 분석을 추가로 할 수 있음

반복이 있는 이원배치법의 데이터 구조식은 다음과 같음

$$\tag{11.7} Y_{ijk} = \mu_{ij}+\varepsilon_{ijk}, \,\, i = 1,2,\dots,a; \,\, j=1,2,\dots,b; \,\, k=1,2,\dots,r\\ \mu_{ij} = \mu + \alpha_i + \beta_j +(\alpha\beta)_{ij}$$

여기서 $\mu_{ij}$는 인자 A의 i수준과 인자 B의 j 수준 조합에서의 평균, $\alpha_i$는 인자 A의 i 수준에 의한 효과, $\beta_j$는 인자 B의 j 수준에 의한 효과, $(\alpha\beta_{ij})$는 두 인자 간의 교호작용을 의미 (전체 결과는 표 11-5와 같음)

<표 11-5> 반복이 있는 이원배치법의 데이터 구조

인자 B \ 인자 A	$\begin{matrix}A_1&&&&A_2&&&&\dots&&&&A_a\end{matrix}$	합	평균
$B_1$	$\begin{matrix}\begin{matrix}Y_{111}\\Y_{112}\\\vdots\\Y_{11r}\end{matrix} \Bigg\}T_{11.}&&\begin{matrix}Y_{211}\\Y_{212}\\\vdots\\Y_{21r}\end{matrix} \Bigg\}T_{21.} &&\begin{matrix}\dots\\\dots\\\\\dots\end{matrix}&& \begin{matrix}Y_{a11}\\Y_{a12}\\\vdots\\Y_{a1r}\end{matrix} \Bigg\}T_{a1.}\end{matrix}$	$T_{.1.}$	$\bar Y_{.1.}$
$B_2$	$\begin{matrix}\begin{matrix}Y_{121}\\Y_{122}\\\vdots\\Y_{12r}\end{matrix} \Bigg\}T_{12.}&&\begin{matrix}Y_{221}\\Y_{222}\\\vdots\\Y_{22r}\end{matrix} \Bigg\}T_{22.} &&\begin{matrix}\dots\\\dots\\\\\dots\end{matrix}&& \begin{matrix}Y_{a21}\\Y_{a22}\\\vdots\\Y_{a2r}\end{matrix} \Bigg\}T_{a2.}\end{matrix}$	$T_{.2.}$	$\bar Y_{.2.}$
$\vdots$	$\begin{matrix}\vdots&&&&\vdots&&&&\vdots&&&&\vdots \end{matrix}$
$B_b$	$\begin{matrix}\begin{matrix}Y_{1b1}\\Y_{1b2}\\\vdots\\Y_{1br}\end{matrix} \Bigg\}T_{1b.}&&\begin{matrix}Y_{2b1}\\Y_{2b2}\\\vdots\\Y_{2br}\end{matrix} \Bigg\}T_{2b.} &&\begin{matrix}\dots\\\dots\\\\\dots\end{matrix}&& \begin{matrix}Y_{ab1}\\Y_{ab2}\\\vdots\\Y_{abr}\end{matrix} \Bigg\}T_{ab.}\end{matrix}$	$T_{.b.}$	$\bar Y_{.b.}$
합	$\begin{matrix}T_{1..}&&T_{2..}&&\dots&&T_{a..}\end{matrix}$	$T$
평균	$\begin{matrix}\bar Y_{1..}&&\bar Y_{2..}&&\dots&&\bar Y_{a..}\end{matrix}$		$\bar Y_{...}$

전체 제곱합을 요인별로 분해하기 위해 우선 SST가 다음과 같이 됨을 보일 수 있음

$$\small{SST = \sum_{i=1}^a \sum_{j=1}^b\sum_{k=1}^r(Y_{ijk} - \bar Y_{\dots})^2 = r\sum_{i=1}^a\sum_{j=1}^b(\bar Y_{ij.} - \bar Y_{\dots})^2 + \sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^r(Y_{ijk}-\bar Y_{ij.})^2} \quad\quad \quad\tag{11.8}$$

위 식의 두 번째 항은 오차제곱합을 나타내며, 첫 번째 항은 각 처리조건에 대한 평균과 전체 평균과의 차에 대한 제곱합이므로 이를 처리제곱합 (treatment sum of squares; SSTR)이라 한다

즉,

$$\tag{11.9} SSTR = r\sum_{i=1}^a\sum_{j=1}^b(\bar Y_{ij.}-\bar Y_{...})^2$$

따라서 식 11.8의 전체 제곱합은 다음과 같이 분해된다

$$\tag{11.10} SST = SSTR + SSE$$

그리고 식 11.9에 관련관 $\bar Y_{ij.} - \bar Y_{...}$이 다음과 같이 표현되므로

$$\bar Y_{ij.} - \bar Y_{...} = [a\,효과]\,(\bar Y_{i..} - \bar Y_{...}) + [b \,효과]\,(\bar Y_{.j.} - \bar Y_{...}) + [a와\,b의\,교호작용]\,(\bar Y_{ij.} - \bar Y_{i..}-\bar Y_{.j.} + \bar Y_{...})$$

처리제곱합 SSTR은 다음과 같이 인자 A의 제곱합(SSA), 인자 B의 제곱합(SSB), 인자 AB의 교호작용 제곱합(SSAB)로 분해됨

$$\tag{11.11} SSTR = SSA + SSB + SSAB$$

결국 전체제곱합은 다시 다음과 같이 분해된다고 볼 수 있음

$$\tag{11.12} SST = SSA + SSB + SSAB + SSE$$

각 요인별 제곱합을 산출하기 위해 다음 식들을 이용하면 편리

$$\tag{11.13a} SST = \sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^rY_{ijk}^2 - CT$$

$$\tag{11.13b} SSTR = \frac{1}{r}\sum_{i=1}^a\sum_{j=1}^bT_{ij.}^2 - CT$$

$$\tag{11.13c} SSE = SST - SSTR$$

$$\tag{11.13d} SSA = \frac{1}{br}\sum_{i=1}^aT_{i..}^2 - CT$$

$$\tag{11.13e} SSB = \frac{1}{ar}\sum_{j=1}^bT_{.j.}^2 - CT$$

$$\tag{11.13f} SSAB = SSTR - SSA - SSB$$

여기서 CT는 수정항(correction term)으로 다음과 같이 주어짐

$$\tag{11.14} CT = \frac{T^2}{abr}$$

<표 11-6> 반복이 있는 이원배치법의 분산분석표

변동요인	제곱합	자유도	평균제곱	$F-$값
인자 A	$SSA$	$a-1$	$MSA=SSA/(a-1)$	$F_A=MSA/MSE$
인자 B	$SSB$	$b-1$	$MSB=SSB/(b-1)$	$F_B=MSB/MSE$
교호작용	$SSAB$	$(a-1)(b-1)$	$MSAB=SSAB/((a-1)(b-1))$	$F_{AB}=MSAB/MSE$
오차	$SSE$	$ab(r-1)$	$MSE=SSE/(ab(r-1))$
전체	$SST$	$ab-1$

각 요인에 대한 가설과 검정방법

1. 인자 A의 효과에 대한 검정

   $$\tag{11.15} \begin{aligned} H_0 &: \alpha_0 = \alpha_2 = \dots = \alpha_a = 0 \\ H_1 &: 모든\,\,\alpha_i가\,\,0은\,\,아니다. \end{aligned}$$

   검정통계량 $F_A = MSA/MSE의 값이 $F_{(\alpha;\,a-1,ab(r-1))}$보다 크면 귀무가설 기각

2. 인자 B의 효과에 대한 검정

   $$\tag{11.16} \begin{aligned} H_0 &: \beta_0 = \beta_2 = \dots = \beta_b = 0 \\ H_1 &: 모든\,\,\beta_i가\,\,0은\,\,아니다. \end{aligned}$$

   검정통계량 $F_B = MSB/MSE$의 값이 $F_{(\alpha;\,b-1,ab(r-1))}$보다 크면 귀무가설 기각

3. 교호작용에 대한 검정

   $$\tag{11.17} \begin{aligned} H_0 &: (\alpha\beta){ij} = 0\,\,(모든\,i와\,j에\,대해) \\ H_1 &: 모든\,\,(\alpha\beta){ij}가\,\,0은\,\,아니다. \end{aligned}$$

   검정통계량 $F_{AB} = MSAB/MSE$값이 $F_{(\alpha; (a-1)(b-1), ab(r-1))}$보다 크면 귀무가설 기각 $\rarr$ 교호작용 있음

반복이 있는 이원배치법에서는 우선 인자간의 교호작용이 있는가를 검정하고 교호작용이 유의하지 않은 경우에는 교호작용을 오차항과 합하여 풀링한 오차제곱합을 이용하여 검정할 수 있음

표 11-4와 표 11-6에서 반복이 없는 경우 (r=1)은 원래 오차항의 자유도는 0이 되는데 교호작용의 제곱합을 오차의 제곱합으로 간주한 것

또한 반복이 없는 이원배치법에 대해서도 r=1로 놓고 식 11.13과 식 11.14를 적용하여 제곱합을 산출할 수 있음

단, 반복이 없는 실험에서는 그 실험에서의 최고차 교호작용(여기서는 SSAB)를 오차(SSE)로 간주

11.4 요인배치법

인자의 수가 $n$이고 각 수준수가 $k$개인 실험계획법을 $k^n$ 요인배치법(factorial design)이라 한다 인자 A,B,C가 있고 각 수준이 2개씩이라면 $2^3$ 요인배치법이 되고, 인자가 두 개이고 각 수준이 3이면 $3^2$ 요인배치법이 됨

요인배치법은 모든 인자의 주효과뿐만 아니라 모든 가능한 교호작용을 검정하고자 할 때 효과적 요인배치법은 다원배치법의 특수한 형태인데 그 분석방법이 단순하기 때문에 널리 사용

그러나 요인의 수가 많은 경우에는 실험조건이 많아지므로 시간 및 비용의 고려도 필요

11.4.2 $2^2$ 요인배치법

$2^2$요인배치법은 인자가 A,B 두 개이며 각 인자의 수준이 2개인 실험으로 이원배치법의 특수한 형태미으로 모형은 기본적으로 식 11.7과 동일

$$\tag{11.18} \begin{aligned} Y_{ijk} &= \mu_{ij} + \varepsilon_{ijk},\,\,i=0,1;\,j=0,1;\,k=1,2,\dots,r \\ \mu_{ij} &= \mu + \alpha_i + \beta_j + (\alpha\beta)_{ij} \end{aligned}$$

각 인자가 두 수준을 갖기 때문에 편의상 첫 수준을 0, 두번째 수준을 1로 나타냄

인자 A의 i 수준에서의 평균을 $\mu_i.$, 인자 B의 수준 j에서 평균을 $\mu_{.j}$라 하면 다음과 같이 표현

$$\mu_{i.} = \mu + \alpha_i \\ \mu_{.j} = \mu + \beta_j$$

식 11.18의 $\mu_{ij}$는 다음과 같다

$$\tag{11.19} \mu_{ij} = \mu_{i.} + \mu_{.j} - \mu + (\alpha\beta)_{ij}$$

전체 데이터 구조는 표 11.7과 같다

<표 11.7> $2^2$요인배치법의 데이터 구조

	$A_0$	$A_1$	합
$B_0$	$\begin{matrix}Y_{001}\\\vdots\\Y_{00r}\end{matrix}\Big\}T_{00.}$	$\begin{matrix}Y_{101}\\\vdots\\Y_{10r}\end{matrix}\Big\}T_{10.}$	$T_{.0.}$
$B_1$	$\begin{matrix}Y_{011}\\\vdots\\Y_{01r}\end{matrix}\Big\}T_{01.}$	$\begin{matrix}Y_{111}\\\vdots\\Y_{11r}\end{matrix}\Big\}T_{11.}$	$T_{.1.}$
합계	$T_{0..}$	$T_{1..}$	$T$

분석방법은 11.3.2절의 반복이 있는 이원배치법과 동일한 방식을 이용할 수 있지만 아래 결과를 이용하면 보다 간단하게 각 요인의 제곱합을 구할 수 있음

인자 A의 주효과는 수준 $A_1$과 수준 $A_0$에서의 평균반응치의 차이므로 다음과 같고

$$인자\,\,A\,\,주효과 = \mu_{1.} - \mu_{0.} = \alpha_{1} - \alpha_{0}$$

다음 식으로 추정 가능

$$\tag{11.20} A\,\,주효과 = \frac{1}{2r}[T_{1..} - T_{0..}]$$

식 11.20에서 $\mu_{i.}$을 $T_{i..}/2r$로 추정 마찬가지로 인자 B의 주효과는 $\mu_{.1} - \mu_{.0} = \beta_1 - \beta_0$이며 다음과 같이 추정할 수 있음

$$\tag{11.21} B \,\, 주효과 = \frac{1}{2r}[T_{.1.} - T_{.0.}]$$

인자 간의 교호작용이 있다는 것은 수준 $A_1$에서의 인자 B의 두 수준 간의 반응치 차이가 수준 $A_0$에서의 인자 B의 두 수준간의 반응치 차이와 서로 다름을 의미 $\rarr$ 교호작용효과는 다음과 같이 표현

$$AB\,교호작용 = \frac{(\mu_{11}-\mu_{10})-(\mu_{01}-\mu_{00})}{2} = \frac{\{(\alpha\beta){11}-(\alpha\beta){10}\} - \{(\alpha\beta){01}-(\alpha\beta){00}\}}{2}$$

따라서 아래와 같이 추정할 수 있다

$$\tag{11.22} \begin{aligned} AB \,\, 교호작용 &= \frac{1}{2r}[(T_{11.} - T_{10.}) - (T_{01.} - T_{00.})] \\ &= \frac{1}{2r}[T_{11.} + T_{00.} - T_{10.} - T_{01.}] \end{aligned}$$

각 요인에 대한 제곱합은 위에서 계산된 각 효과의 제곱에 $r$을 곱합으로써 다음과 같이 산출된다

$$\tag{11.23a} SSA = r(A 주효과)^2 = \frac{1}{4r}(T_{1..} - T_{0..})^2$$

$$\tag{11.23b} SSB = r(B 주효과)^2 = \frac{1}{4r}(T_{.1.} - T_{.0.})^2$$

$$\tag{11.23c} SSAB = r(AB교호작용)^2$$

위 식에서 분모의 $4r$은 전체 실험 수

전체제곱합 SST는 다음식으로부터 산출됨

$$\tag{11.24} SST = \sum_{i=0}^1\sum_{j=0}^1\sum_{k=1}^rY_{ijk}^2 -\frac{T^2}{4r}$$

따라서 오차제곱합은 아래와 같다

$$SSE = SST - (SSA + SSB + SSAB)$$

<표 11.8> $2^2$ 요인배치법의 분산분석표

변동요인	제곱합	자유도	평균제곱	$F-$값
A	$SSA$	1	$MSA=SSA/1$	$F_A = MSA/MSE$
B	$SSB$	1	$MSB=SSB/1$	$F_B = MSB/MSE$
AB	$SSAB$	1	$MSAB=SSAB/1$	$F_{AB} = MSAB/MSE$
오차	$SSE$	$4(r-1)$	$MSE=SSE/(4(r-1))$
전체	$SST$	$4r-1$

인자 A의 효과, 인자 B의 효과, 교호작용에 대한 검정은 각각 식 11.15, 11.16, 11.17과 같으며 검정과정은 반복이 없는 이원배치법의 경우와 동일

각 수준 조합 내 반복이 없는 경우 교호작용과 오차를 서로 분리하여 검출할 수 없으며 따라서 주효과에 대한 검정만 가능

11.4.2 $2^3$ 요인배치법

$2^3$ 요인배치법은 인자가 A,B,C 3개이고 각 인자의 수준이 2개인 실험

반복수가 r일 때 모형은 다음과 같다

$$\small{ Y_{ijkm} = \mu + \alpha_i + \beta_j + \gamma_k + (\alpha\beta){ij} + (\beta\gamma){jk} + (\alpha\gamma){ik} + (\alpha\beta\gamma){ijk} + \varepsilon_{ijkm}, \\ (i,j,k = 0,1;\,\,m=1,2,\dots,r)}\\ \quad\quad \tag{11.25}$$

여기서 $\gamma_k$는 인자 C의 수준 k에서의 효과를 나타내며 $(\beta\gamma){jk}$는 인자 B와 C의 교호작용, $(\alpha\beta\gamma){ijk}$는 인자 A,B,C의 3차 교호작용을 의미

각 인자의 첫 수준을 0, 두 번째 수준을 1로 나타내면 각 실험처리조합의 데이터합은 표 11.9와 같이 나타낼 수 있다

<표 11.9> $2^3$ 요인배치법의 데이터 구조

		$A_0$	$A_1$	합
$B_0$	$\begin{matrix}C_0\\C_1\end{matrix}$	$\begin{matrix}T_{000}\\T_{001}\end{matrix}\Big\}T_{00.}$	$\begin{matrix}T_{100}\\T_{101}\end{matrix}\Big\}T_{10.}$	$T_{.0.}$
$B_1$	$\begin{matrix}C_0\\C_1\end{matrix}$	$\begin{matrix}T_{010}\\T_{011}\end{matrix}\Big\}T_{01.}$	$\begin{matrix}T_{110}\\T_{111}\end{matrix}\Big\}T_{11.}$	$T_{.1.}$
합계		$T_{0..}$	$T_{1..}$	$T$

$$\tag{11.26a} A 주효과 = \frac{1}{4r}[T_{1..}-T_{0..}]$$

$$\tag{11.26c} C 주효과 = \frac{1}{4r}[T_{..1}-T_{..0}]$$

$2^3$ 요인배치법에서 AB, AC, BC의 2차 교호작용은 다음과 같이 추정할 수 있다

$$\tag{11.27a} AB\,\,교호작용 = \frac{1}{4r}[T_{11.}+T_{00.}-T_{10.}-T_{01.}]$$

$$\tag{11.27b} AC\,\,교호작용 = \frac{1}{4r}[T_{1.1}+T_{0.0}-T_{0.1}-T_{1.0}]$$

$$\tag{11.27c} BC\,\,교호작용 = \frac{1}{4r}[T_{.11}+T_{.00}-T_{.10}-T_{.01}]$$

ABC 3차 교호작용은 다음과 같이 얻을 수 있음 ABC의 3차 교호작용은 $B_1$수준에서의 AC교호작용과 $B_0$ 수준에서의 AC 교호작용의 차 $B_1$ 수준에서 AC 교호작용은 $(T_{111} - T_{110}) - (T_{011} - T_{010})$과 관련되며 $B_0$ 수준에서의 AC 교호작용은 $(T_{101}-T_{100}) - (T_{001}-T_{000})$ 으로 표현되므로 다음과 같이 나타낼 수 있다

$$\tag{11.28} \begin{aligned} ABC\,\,교호작용 &= \frac{1}{4r}[(T_{111} - T_{110}) - (T_{011} - T_{010}) - \{(T_{101}-T_{100}) - (T_{001}-T_{000})\}] \\ &= \frac{1}{4r}[T_{111} + T_{100} + T_{010} + T_{001}) - T_{011}-T_{101} - T_{110}-T_{000}] \end{aligned}$$

각 인자의 제곱합 및 인자들의 교호작용에 대한 제곱합은 다음과 같은 방식으로 산출된다

$$\tag{11.29a} SSA = 2r(A주효과)^2 = \frac{1}{8r}(T_{1..}-T_{...})^2$$

$$\tag{11.29b} SSB = 2r(B주효과)^2 = \frac{1}{8r}(T_{.1.}-T_{.0.})^2$$

$$\tag{11.29c} SSC = 2r(C주효과)^2 = \frac{1}{8r}(T_{..1}-T_{..0})^2$$

$$\tag{11.29d} SSAB = 2r(AB교호작용)^2$$

$$\tag{11.29e} SSAC = 2r(AC교호작용)^2$$

$$\tag{11.29f} SSBC = 2r(BC교호작용)^2$$

$$\tag{11.29g} SSABC = 2r(ABC교호작용)^2$$

위 식에서 분모의 $8r$은 전체 실험수

전체제곱합은 다음과 같이 계산됨

$$\tag{11.30} SST = \sum_{i=0}^1\sum_{j=0}^1\sum_{k=0}^1\sum_{m=1}^r Y_{ijkm}^2 - \frac{T^2}{8r}$$

위의 결과로부터 얻은 분산분석표는 다음과 같다

<표 11.10> $2^3$요인배치법의 분산분석표

변동요인	제곱합	자유도	평균제곱	$F-$값
A	$SSA$	1	$MSA = SSA/1$	$F_A=MSA/MSE$
B	$SSB$	1	$MSB = SSB/1$	$F_B=MSB/MSE$
C	$SSC$	1	$MSC = SSC /1$	$F_C=MSC/MSE$
AB	$SSAB$	1	$MSAB = SSAB /1$	$F_{AB}=MSAB/MSE$
AC	$SSAC$	1	$MSAC = SSSAC /1$	$F_{AC} = MSAC/MSE$
BC	$SSBC$	1	$MSBC = SSBC /1$	$F_{BC}=MSBC/MSE$
ABC	$SSABC$	1	$MSABC = SSABC /1$	$F_{ABC}=MSABC/MSE$
오차	$SSE$	$8(r-1)$	$MSE=SSE/(8(r-1))$
전체	$SST$	$8r-1$

분석방법은 $2^2$ 요인배치법의 분석방법을 확장한 것으로 유사하게 진행할 수 있음

수준수가 2이고 인자수가 $n$인 $2^n$ 요인배치법의 경우도 유사하게 분석할 수 있음

요인배치법에서 인자의 수 또는 수준수가 증가하면 필요한 실험수는 급격하게 증가함 이 경우 일부 고차의 교호작용을 무시할 수 있다면 교락법(confounding method)을 이용하여 전체 실험처리 중 일부 실험만을 하는 일부실시법을 채택할수도 있음

교락법은 실험전체를 몇 개의 블럭으로 나누는 방법이고 일부실시법은 나누어진 블럭 중 하나를 택하여 실험하는 방법

11.5 수준조합 모평균의 추정

지금까지 주로 분산분석법을 통해 각 인자의 유의성을 검정

본 절에서는 대표적으로 반복이 있는 이원배치법에 대해 수준조합에 대한 모평균을 추정 즉, 인자 A와 B의 $(A_i, B_j)$ 수준조합에 대한 평균반응치가 얼마나 될 것인가를 추정하는 것으로 그 신뢰구간 구하기

특히 $(A_i, B_j)$ 수준조합이 최적조건으로 판정된 경우에는 이와 같은 추정이 필요함

식 11.7로 주어진 반복이 있는 이원배치법에 대한 모형을 다시 쓰면 다음과 같다

$$Y_{ijk} = \mu_{ij}+\varepsilon_{ijk}, \,\, i = 1,2,\dots,a; \,\, j=1,2,\dots,b; \,\, k=1,2,\dots,r\\ \mu_{ij} = \mu + \alpha_i + \beta_j +(\alpha\beta)_{ij}$$

위 식에서 $\mu_{ij}$에 대한 신뢰구간을 구하고자 함 교호작용이 무시되지 않는 경우와 무시되는 경우를 나누어 다룸 교호작용에 대한 검정에서 기각되지 않으면 이 교호작용을 무시할 수 있음

11.5.1 교호작용이 무시되지 않는 경우

이 경우 $\mu_{ij}$의 점추정량은 $(A_i, B_j)$ 수준조합에 대한 표본평균으로 다음과 같다

$$\hat \mu_{ij} = \frac{T_{ij.}}{r} = \hat Y_{ij.}$$

이 추정량의 분산은 아래와 같은데

$$Var[\hat \mu_{ij}] = \frac{Var[T_{ij.}]}{r^2} = \frac{\sigma^2}{r}$$

여기서 $\sigma^2$은 MSE로 추정되므로, $\mu_{ij}$에 대한 $100(1-\alpha)\%$ 신뢰구간은 다음과 같다

$$\tag{11.31} \bar Y_{ij.} \pm t_{(\alpha/2;\phi_E)}\sqrt{MSE/r}$$

위 식에서 $\phi_E$는 오차제곱합에 대한 자유도로서 반복이 있는 이원배치법의 경우 $\phi_E = ab(r-1)$이다

11.5.2 교호작용이 무시되는 경우

교호작용이 유의하지 않아 무시되는 경우에는 평균의 추정방법이 약간 다름 이 경우 $\mu_{ij}$는 다음과 같이 표현

$$\mu_{ij} = \mu + \alpha_i + \beta_j = \mu + \alpha_i + \mu + \beta_j - \mu$$

여기서 $\mu + \alpha_i$는 $A_i$ 수준에서의 평균이고, $\mu + \beta_j$는 $B_j$ 수준에서의 평균이므로 $\mu_{ij}$의 점추정량은 다음과 같다

$$\hat \mu_{ij} = \bar Y_{i..} + \bar Y_{.j.} - \bar Y_{...}$$

이 점추정량의 분산은 아래와 같음을 증명할 수 있음

$$\tag{11.32} Var[\hat \mu_{ij}] = \sigma^2(\frac{1}{br} + \frac{1}{ar} - \frac{1}{abr})$$

이 때 $n_e$를 유효반복수(effective number of replication) 이라 하고 다음과 같이 정의하면

$$\tag{11.33} \frac{1}{n_e} = \frac{1}{ar} + \frac{1}{br} - \frac{1}{abr}=\frac{a+b-1}{abr}$$

식 11.32는 다음과 같이 표현된다

$$\tag{11.34} Var[\hat \mu_{ij}] = \frac{\sigma^2}{n_e}$$

따라서 식 11.34에서 $\sigma^2$을 MSE로 추정하면, $\mu_{ij}$에 대한 $100(1-\alpha)\%$ 신뢰구간은 다음과 같다

$$\tag{11.35} \bar Y_{i..} + \bar Y_{.j.} - \bar Y_{...} \pm t_{(\alpha/2;\phi_E)}\sqrt{MSE/n_e}$$

위 식에서 $\phi_E$는 오차제곱합에 대한 자유도로서 반복이 있는 이원배치법의 경우 $\phi_E = ab(r-1)$이다

식 11.35는 반복이 없는 이원배치법의 경우에도 r=1을 대입하여 적용할 수 있음 단, 오차제곱합의 자유도는 $\phi_E = (a-1)(b-1)$

Uploaded by N2T